Mình cần phần cuối ạ
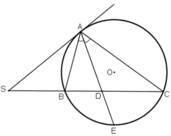
Cho đường tròn (O) và một điểm S nằm ngoài đường tròn. Kẻ tiếp tuyến SA và cát tuyến SBC (B nằm giữa S và C) của đường tròn (O). Gọi I là trung điểm của BC.
l). Chứng minh bốn điểm S, A, O, I củng thuộc một đường tròn.
2) Qua A kẻ đường thẳng vuông góc với SO tại H. Chứng minh SA^2 = SH.SO.
3) Đường thẳng AH cắt BC tại K, cắt (O) tại D. Chứng minh SD là tiếp tuyến của (O).
4). Qua 1 kẻ đường kính PQ của (O) (A và P nằm cùng phía đối với đường thăng SO). Gọi M là giao điểm của SP với (O). Chứng minh SA^2= SK.SI và ba điểm M, K, Q thắng
hàng.

 là góc có đỉnh nằm bên trong đường tròn
là góc có đỉnh nằm bên trong đường tròn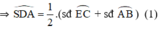
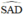 là góc tạo bởi tiếp tuyến AS và dây AE
là góc tạo bởi tiếp tuyến AS và dây AE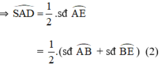
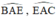 lần lượt là các góc nội tiếp chắn các cung
lần lượt là các góc nội tiếp chắn các cung 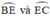
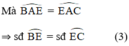
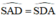
1:
ΔOBC cân tại O
mà OI là trung tuyến
nên OI vuông góc BC
góc OIS=góc OAS=90 độ
=>OIAS nội tiếp
2:
Xet ΔSAO vuông tại A có AH là đường cao
nên SH*SO=SA^2
3:
ΔOAD cân tại O
mà OS là đường cao
nên OS là phân giác của góc AOD
Xét ΔAOS và ΔDOS co
OA=OD
góc AOS=góc DOS
OS chung
=>ΔAOS=ΔDOS
=>góc SDO=90 độ
=>SD là tiếp tuyến của (O)
4: Xet ΔSAK và ΔSIA có
góc SAK=góc SIA
gó ASK chung
=>ΔSAK đồng dạng với ΔSIA
=>SA/SI=SK/SA
=>SA^2=SK*SI