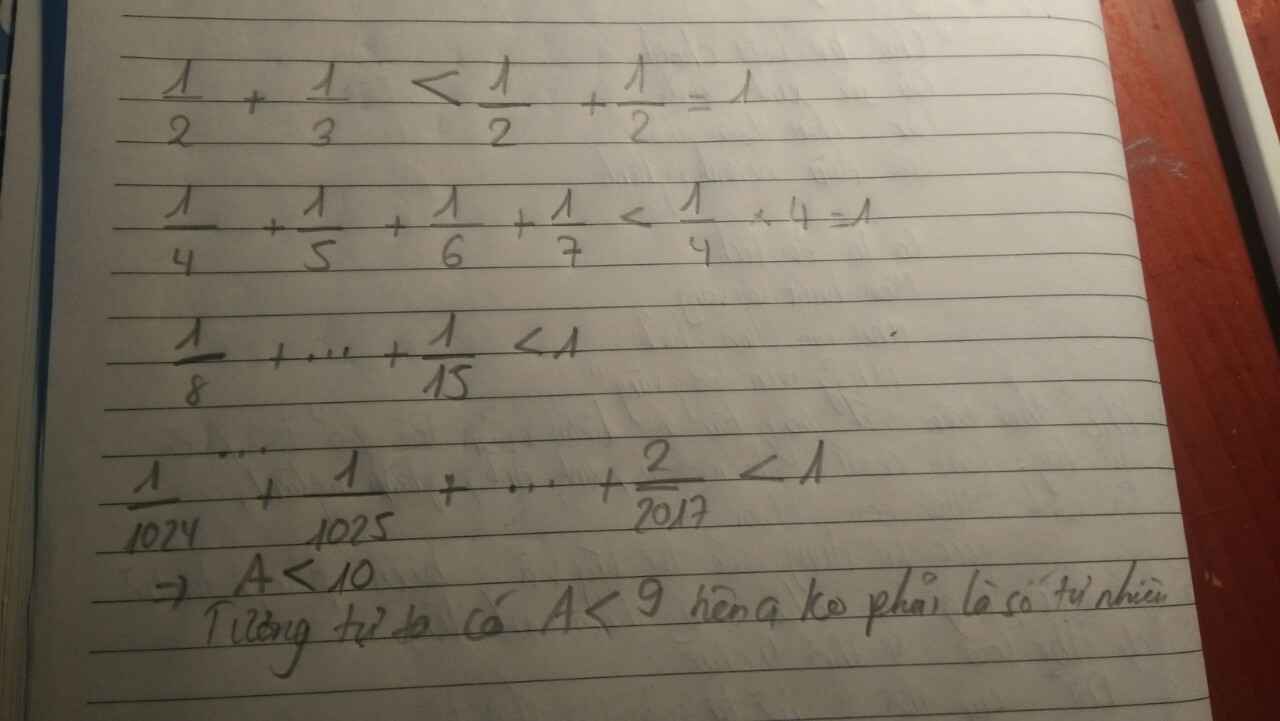Cho A=1/2^2 + 1/3^2 + 1/4^2 +....+ 1/2017^2 Chứng minh A không phải là số nguyên
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
12 tháng 12 2018
\(\frac{3}{4}A=\frac{3}{4}-\left(\frac{3}{4}\right)^2+\left(\frac{3}{4}\right)^3-\left(\frac{3}{4}\right)^4+...-\left(\frac{3}{4}\right)^{2018}+\left(\frac{3}{4}\right)^{2019}\)
\(\frac{3}{4}A+A=\frac{3}{4}-\left(\frac{3}{4}\right)^2+\left(\frac{3}{4}\right)^3-\left(\frac{3}{4}\right)^4+...-\left(\frac{3}{4}\right)^{2018}+\left(\frac{3}{4}\right)^{2019}+1-\frac{3}{4}+\left(\frac{3}{4}\right)^2...\)( Bn tự ghi lại A do máy mình ko đủ độ rộng )
\(\frac{7}{4}A=\left(\frac{3}{4}\right)^{2019}+1\)
\(A=\text{ }\left[\left(\frac{3}{4}\right)^{2019}+1\right]:\frac{7}{4}\)
\(A=\text{ }\frac{\left[\left(\frac{3}{4}\right)^{2019}+1\right].4}{7}\)
=> A là phân số
=> A ko phải số nguyên
HT
0
1 tháng 11 2017
bài 3 : ko vì tổng của hai số nguyên tố là 2003 nên
Trong đó phải có 1 số chẵn và một số lẻ
Mà số nguyên tố duy nhất chẵn là số 2
=> Số còn lại bằng 2001 mà 2001 chia hết cho 3 nên nó là hợp số
PN
3
EG
23 tháng 7 2018
Ta có:
A= 1+1/2+1/4+1/8+....+1/256
Đặt 1/2+1/4+1/8+...+1/256 là S.
Ta có:
S = 1/2+1/4+1/8+...+1/256
2S=1+1/2+1/4+....+1/128
2S-S= 1+1/2+1/4+....+1/128 - 1/2-1/4-1/8-...-1/256
S=1-1/256
S= 255/256
=> S không là số nguyên
S+1 = \(1\frac{255}{256}\)=A
=> A không là số nguyên
Vậy A không phải là số nguyên
23 tháng 7 2018
Cho \(B=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+...+\frac{1}{128}+\frac{1}{256}\)
\(\Rightarrow2B=1+\frac{1}{2}+\frac{1}{4}+...+\frac{1}{128}\)
\(\Rightarrow2B-B=1-\frac{1}{256}\)
\(\Rightarrow B=1-\frac{1}{256}< 1\)
\(\Rightarrow1+1-\frac{1}{256}< 1+1=2\)
Thay B vaof A
\(A=1+1-\frac{1}{256}< 1+1=2\)
\(\Rightarrow A< 2\)
maf \(A=1+\left(1-\frac{1}{256}\right)>1\)
=> \(1< A=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+...+\frac{1}{256}< 2\)
=> A khong phai la so tu nhien