Cho tam giác ABC vuông ở A, AB = 6, BC = 10; đường cao AH, phân giác BD. Gọi I là giao điểm của AH và BD. a) Tính diện tích tam giác ABC, tính AD, DC b) Chứng minh ∆𝐴𝐵𝐶 ∽ △ 𝐻𝐶𝐴 c) Chứng minh 𝐼𝐻 𝐼𝐴 = 𝐴𝐷 𝐷𝐶
d) Chứng minh: AB.BI=BD.HB và tam giác AID cân
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HD
1

NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 12 2021
Áp dụng định lý Pitago:
\(AC=\sqrt{BC^2-AB^2}=8\left(cm\right)\)
\(\Rightarrow S_{ABC}=\dfrac{1}{2}AB.AC=24\left(cm^2\right)\)

5 tháng 2 2022
a: AB=8cm
b: xét ΔABE vuông tại A và ΔDBE vuông tại D có
BE chung
BA=BD
Do đó: ΔABE=ΔDBE
HS
3

D
18 tháng 4 2017
Áp dụng định lý Pitago vào tam giác ABC vuông tại A, có:
\(AC^2+AB^2=BC^2\)
\(\Rightarrow AC^2=BC^2-AB^2\)
\(=10^2-6^2=100-36=64\)
\(\Rightarrow AC=\sqrt{64}=8\)
Ta có: BC>AC>AB
Áp dụng định lí quan hệ giữa góc và cạnh đối diện, ta có:
\(\widehat{A}>\widehat{B}>\widehat{C}\)
LA
7
LA
3

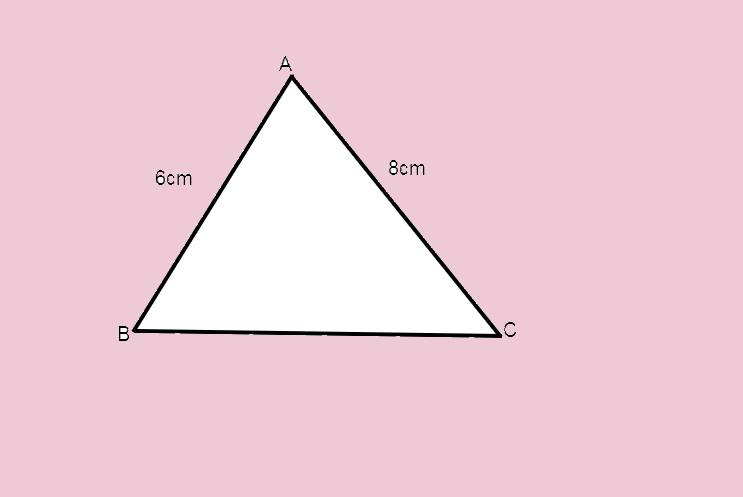
a: \(AC=\sqrt{10^2-6^2}=8\left(cm\right)\)
S ABC=1/2*6*8=3*8=24cm2
Xet ΔABC có BD là phân giác
nên AD/AB=CD/BC
=>AD/3=CD/5=8/8=1
=>AD=3cm; CD=5cm
b: Xét ΔABC vuông tại A và ΔHCA vuông tại H co
góc C chung
=>ΔABC đồng dạngvới ΔhAC
c: IH/IA=BH/BA
AD/DC=BA/BC
mà BH/BA=BA/BC
nên IH/IA=AD/DC
d:
góc AID=góc BIH=góc ADB=góc ADI
=>ΔADI can tại A