Cho tam giác ABC vuông tại A có BD là tia phân giác của ABC(D thuộc AC).Trên cạnh BC lấy điểm E cho BE = BA
a. Chứng minh tam giác ABD bằng tam giác EBD
b. Gọi O là giao điểm của AE và BD .chứng minh OA = OE
Giúp mik nha mik đag cần gấp
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
A
Ar 🐶
19 tháng 3 2023
Đúng(1)
Những câu hỏi liên quan
16 tháng 4 2023
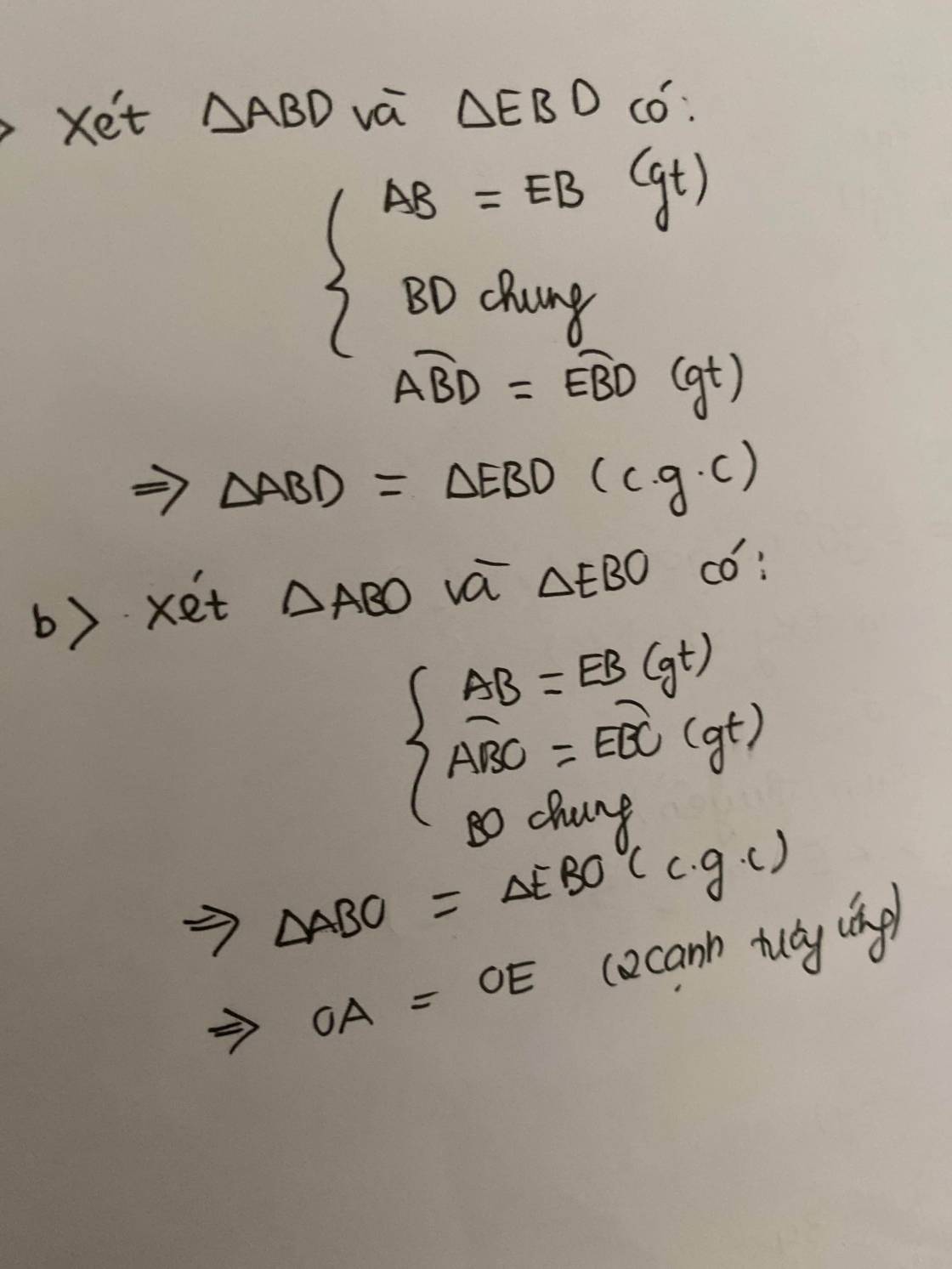
a: Xét ΔBAD và ΔBED có
BA=BE
góc ABD=góc EBD
BD chung
=>ΔBAD=ΔBED
b: ΔBAD=ΔBED
=>góc BED=90 độ
=>DE vuông góc CB
c: BA=BE
DA=DE
=>BD là trung trực của AE
d: Xét ΔDAF vuông tại A và ΔDEC vuông tại E có
DA=DE
AF=EC
=>ΔDAF=ΔDEC
=>góc ADF=góc EDC
=>góc ADF+góc ADE=180 độ
=>F,D,E thẳng hàng
5 tháng 1 2022
a: Xét ΔABD và ΔEBD có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔABD=ΔEBD
b: Ta có: ΔABD=ΔEBD
nên DA=DE
Ta có: ΔABD=ΔEBD
nên \(\widehat{BAD}=\widehat{BED}=90^0\)
hay DE⊥BC
17 tháng 2 2022
a: Xét ΔABD và ΔEBD có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔABD=ΔEBD
b: Ta có: ΔBAD=ΔBED
nên \(\widehat{BAD}=\widehat{BED}=90^0\)
hay DE\(\perp\)BC
c: Xét ΔADK vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADK}=\widehat{EDC}\)
Do đó: ΔADK=ΔEDC
Suy ra: AK=EC
Ta có: BA+AK=BK
BE+EC=BC
mà BA=BE
và AK=EC
nên BK=BC
4 tháng 1 2023
a: Xét ΔBAD và ΔBED có
BA=BE
góc ABD=góc EBD
BD chung
Do đó: ΔBAD=ΔBED
=>BA=BE
=>ΔBAE cân tại B
b: ΔBAD=ΔBED
=>góc BED=90 độ
=>DE vuông góc với BC
c: ΔBAD=ΔBED
=>BA=BE và DA=DE
=>BD là trung trực của AE
4 tháng 1 2023
nếu bạn không phiền thì có thể vẽ hình ra được không ạ :((
3 tháng 1 2022
a: Xét ΔABD và ΔEBD có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔABD=ΔEBD
b: Ta có: ΔABD=ΔEBD
Suy ra: DA=DE
Ta có: ΔABD=ΔEBD
nên \(\widehat{BAD}=\widehat{BED}=90^0\)
hay DE⊥BC
c: Ta có: BE=BA
nên B nằm trên đường trung trực của EA(1)
Ta có: DE=DA
nên D nằm trên đường trung trực của EA(2)
Từ (1) và (2) suy ra BD là đường trung trực của EA
4 tháng 1 2022
a: Xét ΔABD và ΔEBD có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔABD=ΔEBD
b: Ta có: ΔABD=ΔEBD
nên DA=DE
hay D nằm trên đường trung trực của AE(1)
Ta có: BA=BE
nên B nằm trên đường trung trực của AE(2)
Từ (1) và (2) suy ra BD là đường trực của AE
hay BD⊥AE
c: Xét ΔADF vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADF}=\widehat{EDC}\)
Do đó: ΔADF=ΔEDC
Suy ra: AF=EC
18 tháng 8 2022
Bài 3:
a: Xét ΔABM và ΔACN có
AB=AC
góc ABM=góc ACN
BM=CN
Do đó: ΔABM=ΔACN
Suy ra: AM=AN
b: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc BAH=góc CAK
Do đó; ΔAHB=ΔAKC
Suy ra: AH=AK và BH=CK
c: Xét ΔHBM vuông tại H và ΔKCN vuông tại K có
MB=CN
góc M=góc N
Do đó ΔHBM=ΔKCN
Suy ra: góc HBM=góc KCN
=>góc OBC=góc OCB
hay ΔOBC can tại O