vẽ hình và làm chi tiết nhất
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 6 2023
a: Xét ΔMEI vuông tại M và ΔHEI vuông tại H có
EI chung
góc MEI=góc HEI
=>ΔMEI=ΔHEI
b: EM=EH và IM=IH
=>EI là trung trực của MH
c: góc MIE=góc FIK=60 độ
=>góc FKI=30 độ
Xét ΔHKI vuông tại H và ΔFKI vuông tại F có
KI chung
góc HKI=góc FKI
=>ΔHKI=ΔFKI
=>KH=KF
Xét ΔIEK có góc IEK=góc IKE
nên ΔIEK cân tại I
mà IH là đường cao
nên H là trung điểm của EK
=>HE=KH=FK
d: IK=IE
IE>IM
=>IK>IM
e: Gọi A là giao của FK và EM
Xét ΔEAK có
EF,KM là đường cao
EF cắt KM tại I
=>I là trực tâm
=>AI vuông góc EK
=>A,I,H thẳng hàng
=>EM,Hi,KF đồng quy
21 tháng 7 2023
a: Xét ΔMHC và ΔMKB có
MH=MK
góc HMC=góc KMB
MC=MB
=>ΔMHC=ΔMKB
b: ΔMHC=ΔMKB
=>BK=HC<MC
c: Xét ΔCAB có
M là trung điểm của CB
MH//AB
=>H là trung điểm của AC
Xét ΔCAB có
AM,BH là trung tuyến
AM cắt BH tại G
=>G là trọng tâm
=>C,G,I thẳng hàng
12 tháng 1 2023
Bài 1:
a,b: ΔABC cân tại A
mà AM là trung tuyến
nên AM vừa là đường cao, vừa là phân giác
=>góc BAM=góc CAM và AM vuông góc với BC
c: Xét ΔEBC có
EM vừa là đường cao, vừa là trung tuyến
nên ΔEBC cân tại E
d: Xét ΔKCB có
CE là trung tuyến
CE=KB/2
Do đó: ΔKCB vuông tại C
=>KC//AE
HT
1
15 tháng 10 2023
a: Xét tứ giác AEDF có
\(\widehat{AED}=\widehat{AFD}=\widehat{FAE}=90^0\)
=>AEDF là hình chữ nhật
=>AD cắt EF tại trung điểm của mỗi đường
mà I là trung điểm của EF
nên I là trung điểm của AD
=>A,I,D thẳng hàng
b: Xét ΔBAC có DE//AC
nên \(\dfrac{DE}{AC}=\dfrac{BD}{BC}\)
Xét ΔBAC có DF//AB
nên \(\dfrac{DF}{AB}=\dfrac{CD}{CB}\)
\(\dfrac{DE}{AC}+\dfrac{DF}{AB}=\dfrac{BD}{BC}+\dfrac{CD}{BC}=1\)
=>\(\dfrac{DE}{AB}+\dfrac{DF}{AB}=1\)
=>\(DE+DF=AB\)
=>\(2\cdot\left(DE+DF\right)=2AB\)
=>\(C_{AEDF}=2\cdot AB\) không đổi
TQ
1
25 tháng 1 2018
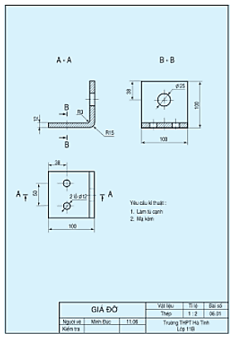
- Bản vẽ chi tiết thể hiện hình dạng, kích thước và yêu cầu kĩ thuật của chi tiết, được dùng để chế tạo và kiểm tra chi tiết.
- Bản vẽ lắp dùng để lắp ráp các chi tiết.
a: XetΔBAD vuông tại A và ΔBHD vuông tại H có
BD chung
góc ABD=góc HBD
=>ΔBAD=ΔBHD
=>BA=BH; DA=DH
mà DH<DC
nên DA<DC
b: Xét ΔBHK vuông tại H và ΔBAC vuông tại A có
BH=BA
góc B chung
=>ΔBHK=ΔBAC
=>BK=BC
c: ΔBKC cân tại B
mà BD là phân giác
nên BD là trung trực của KC
Hình