viết hệ quả talet với tam giác kéo dài
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 1 2021
b) Xét ΔAOB và ΔCOD có
\(\widehat{AOB}=\widehat{COD}\)(hai góc đối đỉnh)
\(\widehat{OAB}=\widehat{OCD}\)(hai góc so le trong, AB//CD)
Do đó: ΔAOB∼ΔCOD(g-g)
⇒\(\dfrac{OA}{OC}=\dfrac{OB}{OD}=\dfrac{AB}{CD}\)(Các cặp cạnh tương ứng)
hay \(\left\{{}\begin{matrix}\dfrac{OA}{OC}=\dfrac{2}{5}\\\dfrac{OB}{OD}=\dfrac{2}{5}\end{matrix}\right.\)
TG
28 tháng 2 2020
Câu 1:
*Định lí Ta - lét thuận: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
*Định lí Ta - lét đảo: Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
Câu 2:
*Định lí Ta - lét đảo: Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
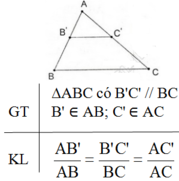
Hệ quả của định lí Talet
Nếu một đường thẳng cắt hai cạnh còn lại của một của một tam giác và song song với các cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh còn lại của tam giác đã cho.
PT
1
CM
28 tháng 8 2019
Hệ quả của định lí Talet:
Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng với tỉ lệ ba cạnh của tam giác đã cho.
9 tháng 1 2022
Chiều cao của tam giác ABC là:
\(30\times2:5=12\left(cm\right)\)
Diện tích tam giác ABC là:
\(24\times12:2=144\left(cm^2\right)\)
Đáp số: 144cm2
xét tam giác ABC có MN//BC(gt)
`=>(AM)/(AB)=(AN)/(AC)=(MN)/(BC)` ( hệ quả talet)