Đốt cháy hoàn toàn hỗn hợp 6,72 lít metan và etilen ở điều kiện tiêu chuẩn sâu phản ứng thu được 8,96 lít khí co2 .
A, tính thành phần % thể tích mỗi khí trong hỗn hợp .
B, tính thể tích oxi đã tham gia phản ứng .
Em cần câu trả lời gấp cảm ơn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 11 2017
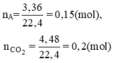
Gọi số mol của metan và etan lần lượt là x và y (mol)
Phương trình phản ứng:
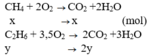
Vậy thành phần phần trăm về thể tích các khí trong hỗn hợp A là:
13 tháng 3 2023
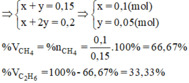
a, \(CH_4+2O_2\underrightarrow{^{t^o}}CO_2+2H_2O\)
\(C_2H_4+3O_2\underrightarrow{^{t^o}}2CO_2+2H_2O\)
b, Gọi: \(\left\{{}\begin{matrix}n_{CH_4}=x\left(mol\right)\\n_{C_2H_4}=y\left(mol\right)\end{matrix}\right.\) \(\Rightarrow x+y=\dfrac{4,48}{22,4}=0,2\left(mol\right)\left(1\right)\)
Theo PT: \(n_{O_2}=2n_{CH_4}+3n_{C_2H_4}=2x+3y=\dfrac{15,68}{22,4}=0,7\left(mol\right)\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\left\{{}\begin{matrix}x=-0,1\\y=0,3\end{matrix}\right.\)
Đến đây thì ra số mol âm, bạn xem lại đề nhé.
17 tháng 3 2023
Ta có: \(n_{Br_2}=\dfrac{6}{160}=0,0375\left(mol\right)\)
PT: \(C_2H_4+Br_2\rightarrow C_2H_4Br_2\)
Theo PT: \(n_{C_2H_4}=n_{Br_2}=0,0375\left(mol\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\%V_{C_2H_4}=\dfrac{0,0375.22,4}{6,72}.100\%=12,5\%\\\%V_{CH_4}=87,5\%\end{matrix}\right.\)
19 tháng 2 2021
- Gọi mol metan và etan là x, y ( mol )
\(x+y=n_{hh}=\dfrac{V}{22,4}=0,25\left(mol\right)\)
Lại có : \(x+2y=n_{CO_2}=\dfrac{V}{22,4}=0,4\left(mol\right)\)
\(\Rightarrow\left\{{}\begin{matrix}x=0,1\\y=0,15\end{matrix}\right.\) ( mol )
\(\Rightarrow\left\{{}\begin{matrix}m_{CH_4}=1,6\left(g\right)\\m_{C_2H_6}=4,5\left(g\right)\end{matrix}\right.\)
=> mhh = 6,1 ( g )
=> %mCH4 = ~ 26,22%
=> %mC2H6 = ~73,78%
Ta có : \(\%V_{CH4}=\dfrac{V}{Vhh}=40\%\)
=> %VC2H6 = 100 - %VCH4 = 60% .
19 tháng 2 2021
PT: \(CH_4+2O_2\underrightarrow{t^o}CO_2+2H_2O\)
\(2C_2H_6+5O_2\underrightarrow{t^o}4CO_2+6H_2O\)
Giả sử: \(\left\{{}\begin{matrix}n_{CH_4}=x\left(mol\right)\\n_{C_2H_6}=y\left(mol\right)\end{matrix}\right.\)
\(\Rightarrow x+y=\dfrac{5,6}{22,4}=0,25\left(1\right)\)
Ta có: \(n_{CO_2}=\dfrac{8,96}{22,4}=0,4\left(mol\right)\)
Theo PT: \(\Sigma n_{CO_2}=n_{CH_4}+2n_{C_2H_6}\)
\(\Rightarrow x+2y=0,4\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\left\{{}\begin{matrix}x=0,1\left(mol\right)\\y=0,15\left(mol\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\%V_{CH_4}=\dfrac{0,1}{0,25}.100\%=40\%\\\%V_{C_2H_6}=60\%\end{matrix}\right.\)
\(\left\{{}\begin{matrix}\%m_{CH_4}=\dfrac{0,1.16}{0,1.16+0,15.30}.100\%\approx26,2\%\\\%m_{C_2H_6}\approx73,8\%\end{matrix}\right.\)
Bạn tham khảo nhé!
23 tháng 3 2023
a, \(CH_4+2O_2\underrightarrow{t^o}CO_2+2H_2O\)
\(2C_2H_2+5O_2\underrightarrow{t^o}4CO_2+2H_2O\)
Ta có: \(n_{CH_4}+n_{C_2H_2}=\dfrac{6,72}{22,4}=0,3\left(mol\right)\left(1\right)\)
\(n_{CO_2}=n_{CH_4}+2n_{C_2H_2}=\dfrac{7,84}{22,4}=0,35\left(mol\right)\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\left\{{}\begin{matrix}n_{CH_4}=0,25\left(mol\right)\\n_{C_2H_2}=0,05\left(mol\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\%V_{CH_4}=\dfrac{0,25.22,4}{6,72}.100\%\approx83,33\%\\\%V_{C_2H_2}\approx16,67\%\end{matrix}\right.\)
Theo PT: \(n_{O_2}=2n_{CH_4}+\dfrac{5}{2}n_{C_2H_2}=0,625\left(mol\right)\Rightarrow m_{O_2}=0,625.32=20\left(g\right)\)
a, PT: \(CH_4+2O_2\underrightarrow{t^o}CO_2+2H_2O\)
\(C_2H_4+3O_2\underrightarrow{t^o}2CO_2+2H_2O\)
Ta có: \(n_{CH_4}+n_{C_2H_4}=\dfrac{6,72}{22,4}=0,3\left(mol\right)\left(1\right)\)
Theo PT: \(n_{CO_2}=n_{CH_4}+2n_{C_2H_4}=\dfrac{8,96}{22,4}=0,4\left(mol\right)\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\left\{{}\begin{matrix}n_{CH_4}=0,2\left(mol\right)\\n_{C_2H_4}=0,1\left(mol\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\%V_{CH_4}=\dfrac{0,2.22,4}{6,72}.100\%\approx66,67\%\\\%V_{C_2H_4}\approx33,33\%\end{matrix}\right.\)
b, Theo PT: \(n_{O_2}=2n_{CH_4}+3n_{C_2H_4}=0,7\left(mol\right)\)
\(\Rightarrow V_{O_2}=0,7.22,4=15,68\left(l\right)\)