Các bn giúp mik với Cho tam giác ABC cân tại A.Từ A kẻ AH vuông góc với BC tại H,trên đoạn thẳng AH lấy điểm M tùy ý(M khác A và H).Chứng minh rằng: a)H là trung điểm BC. b)MB=MC và MH là tia phân giác của góc BMC. c)MB
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A)TA CÓ TAM GIÁC ABC CÂN TẠI A NÊN AB=AC
DO AH VUÔNG GÓC VS BC NÊN HB=HC
SUY RA H LÀ TRUNG ĐIỂM CỦA BC
B)XÉT TAM GIÁC MBH VÀ TAM GIÁC MCH CÓ:
MB=MC(GT)
HB=HC(CMT)
MH LÀ CẠNH CHUNG NÊN HOẶC MH VUÔNG GÓC VS BC
TG MBH=TG MCH (C.C.C)-(CẠNH HUYỀN-CẠNH GÓC VUÔNG)
SUY RA GÓC BMH= GÓC CMH
TA CÓ : BMH+CMH=BMC SUY RA MH LÀ TIA PHÂN GIÁC CỦA GÓC BMC
C)CÒN PHẦN C MỊ CHỊU MỊ CX LƯỜI TÍNH

a: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
b: Xét ΔMCB có
MH vừa là đường cao, vừa là trung tuyến
=>ΔMCB cân tại M
=>MH là phân giác của góc BMC
c: ΔMHB vuông tạiH
=>góc BMH<90 độ
=>góc BMA>90 độ
=>BA>MB

a: ΔABC cân tại A
mà AH là đường cao
nên AH là phân giác của góc BAC và HB=HC
b: Xét ΔABM và ΔACM có
AB=AC
góc BAM=góc CAM
AM chung
Do đó: ΔABM=ΔACM
c: ΔABM=ΔACM
=>MB=MC
d: Vì MB=MC
nên ΔMBC cân tại M

a: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC và AH là trung trựccủaCB
b: SỬa đề; BM=CM
AH là trung trực của BC
=>M nằm trên đường trung trực của BC
=>MB=MC

a)Xét \(\Delta AHB\) vuông tại H và \(\Delta AHC\) vuông tại H có :
\(AB=AC\)
\(\widehat{ABC}=\widehat{ACB}\)
=> \(\Delta AHB\)=\(\Delta AHC\) (ch-gn)
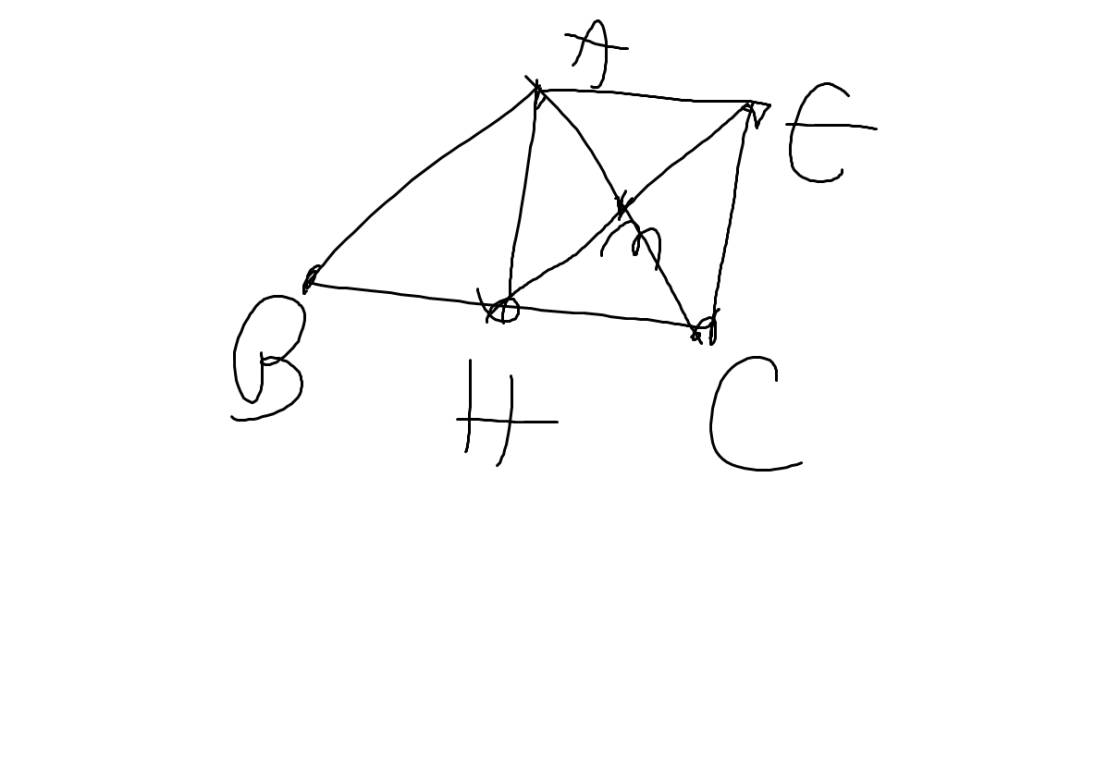
b) Xét \(\Delta AMH\) và \(\Delta CME\) có :
\(AM=MC\)
\(\widehat{AMH}=\widehat{CME}\)
\(ME=MH\)
=> \(\Delta AMH\)=\(\Delta CME\) (c-g-c)
=> AH=CE
c)Có : \(\widehat{HAM}=\widehat{MCE}\)
mà \(\widehat{HAM}và\widehat{MCE}\) ở vị trí so le
=> AH//CE
=> \(\widehat{AHB}=\widehat{HCE}=90^o\)
Xét \(\Delta AHC\) và \(\Delta ECH\) có :
CH chung
\(\widehat{AHB}=\widehat{HCE}=90^o\)
AH=CE
=> \(\Delta AHC\)=\(\Delta ECH\) (c-g-c)
=>\(\widehat{HCA}=\widehat{EHC}\)
mà \(\widehat{HCA}=\widehat{HBA}\)
=> \(\widehat{HBA}=\widehat{EHC}\)
Mà \(\widehat{HBA}và\widehat{EHC}\) ở vị trí đồng vị
=> HM//AB

Ai đó giúp mình với! Mình đang cần gấp!:( Các bạn vẽ hình lun giúp mình nha! Cảm ơn các bạn nhìu!:)
Do tam giác ABC có
AB = 3 , AC = 4 , BC = 5
Suy ra ta được
(3*3)+(4*4)=5*5 ( định lý pi ta go)
9 + 16 = 25
Theo định lý py ta go thì tam giác abc vuông tại A

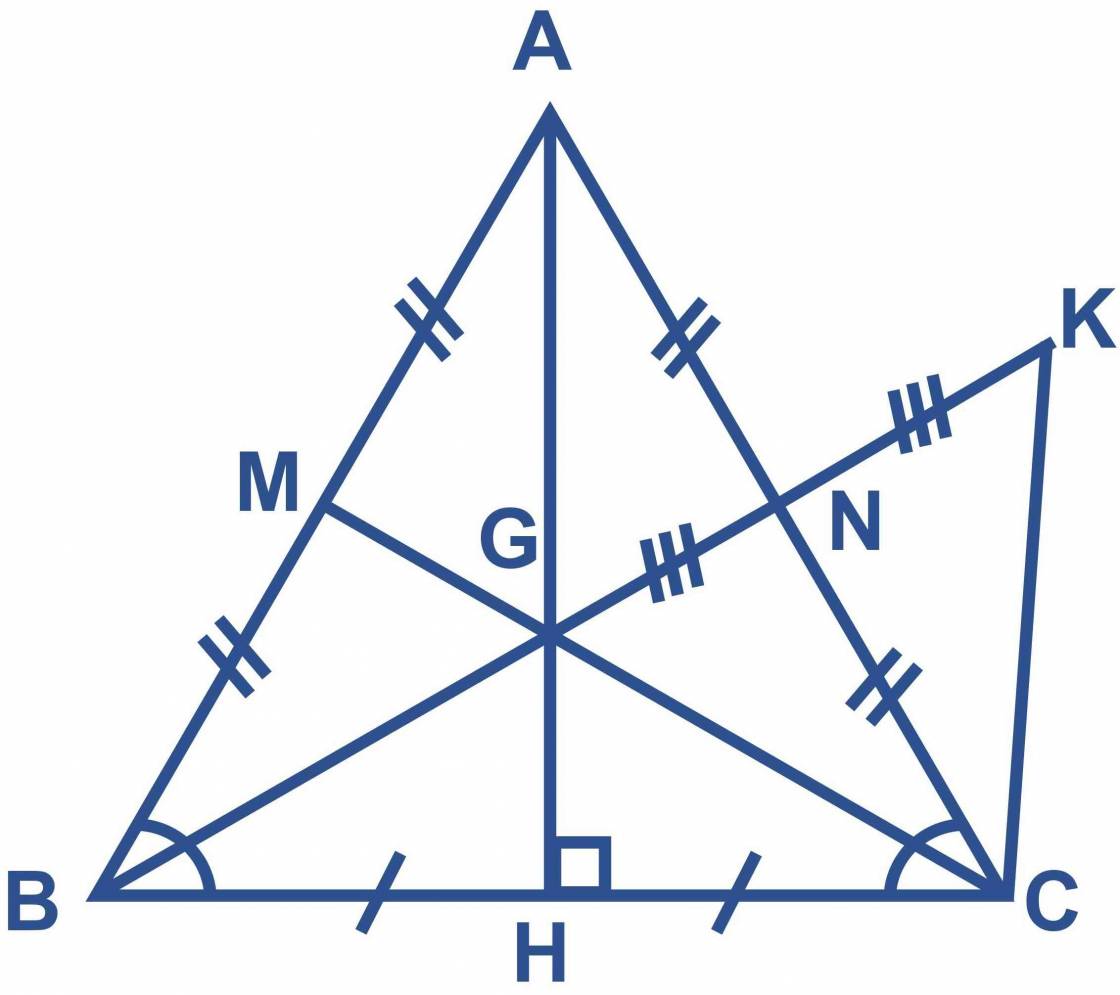
a) trong ΔABC, có góc AHB là góc vuông
góc ABH là góc nhọn
⇒ góc AHB > góc ABH
⇒ AB > AH
b) M là trung điểm của AB và N là trung điểm của AC, mà AB = AC (2 cạnh bên của tam giác cân) ⇒ MB = NC
xét tam giác MBC và tam giác NCB, ta có :
MB = NC (cmt)
góc B = góc C (2 góc đáy của 1 tam giác cân)
BC là cạnh chung
⇒ tam giác MBC = tam giác NCB (c-g-c)
⇒ MC = NB (2 cạnh tương ứng)
c) xét tam giác NAG và tam giác NCK , ta có :
NA = NC (vì N là trung điểm của cạnh AC)
góc NAG = góc NCK (đối đỉnh)
NG = NK (gt)
=> tam giác NAG = tam giác NCK (c-g-c)
=> AG = CK (2 cạnh tương ứng)


a: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
b: Xet ΔMCB có
MH vừa là đường cao, vừa là trung tuyến
=>ΔMCB cân tại M
=>MB=MC
mà MH là đường cao
nên MH là phân giác của góc BMC