Giúp mình trả lời câu này ạ Câu 4 : cho tam giác ABC , các đường cao AH , BK cắt nhau tại E . Chứng minh rằng : A) các điểm C , H , E , K cùng thuộc 1 đường tròn B) ∠HKB = ∠HAB (hai góc bằng nhau)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NL
Nguyễn Lê Phước Thịnh
16 tháng 3 2023
Đúng(1)
Những câu hỏi liên quan
10 tháng 5 2019
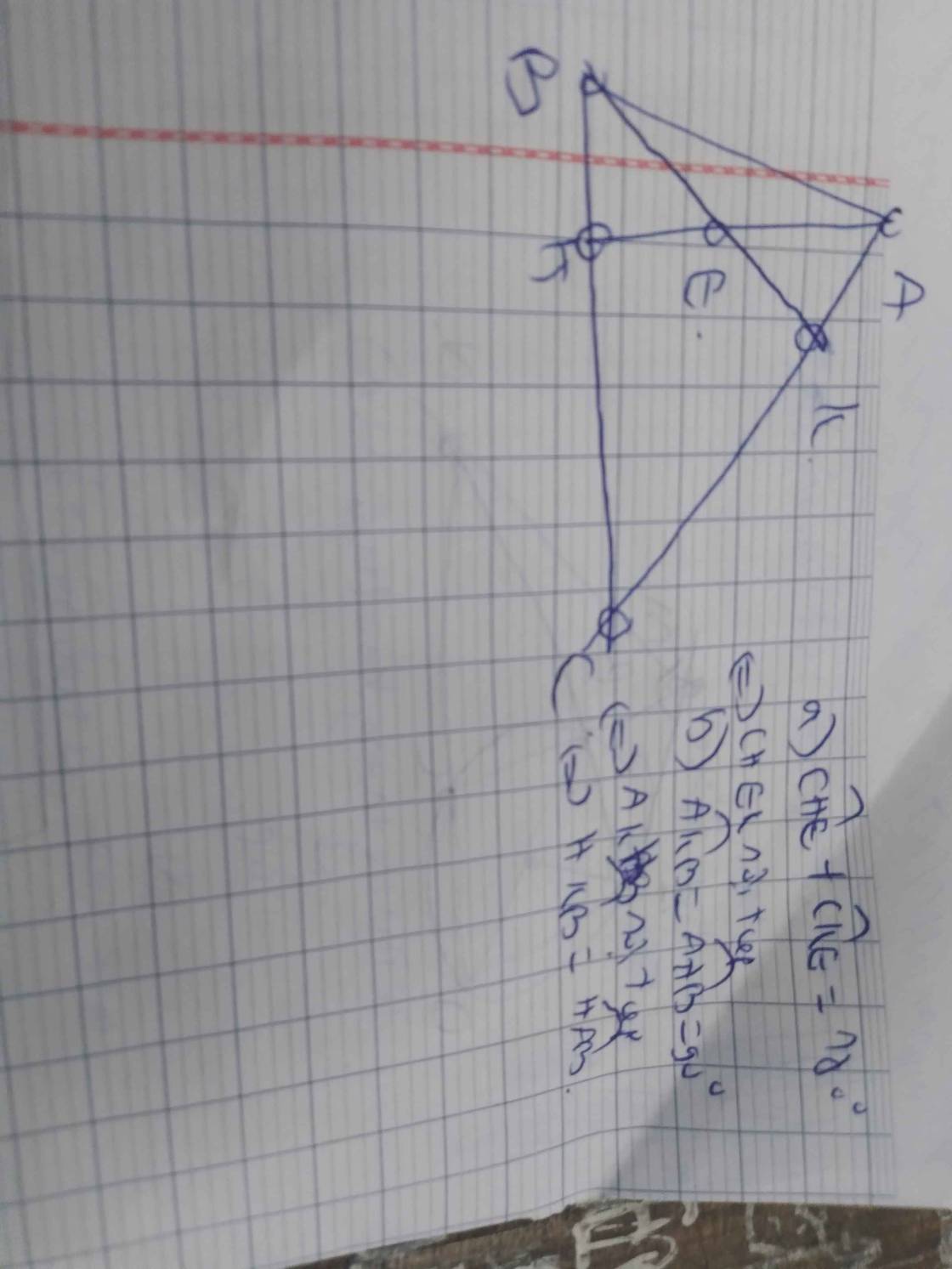
tứ giác BFEC có hai góc kề nhau cùng nhìn đoạn BC dưới một góc vuông : BFCˆ=BECˆ(=90)BFC^=BEC^(=90) ==> Tức giác BFEC là tứ giác nội tiếp
==> 4 điểm B,E,F,C cùng thuộc một đường tròn.
13 tháng 5 2023
b: BE>BC+CE
=BC+1/2CH
=BC+1/2*1/2(HB+HC)
=BC+1/4(HB+HC)>BC+1/4BC
=>BE>5/4BC>3/BC
6 tháng 9 2021
1.Vì BE là đường cao
⇒∠BEC=∠AEB=90o
Tương tự: ∠BFC=∠AFC=90o
Xét tứ giác BFEC có ∠BFC và ∠BEC cùng nhìn BC dưới góc bằng 90o
⇒ BFEC là tứ giác nội tiếp
⇒ 4 điểm B,F,E,C cùng thuộc 1 đường tròn có tâm là trung điểm của BC
2.Xét tứ giác AFHE có ∠AFH + ∠AEH = 90o + 90o =180o
⇒ AFHE là tứ giác nội tiếp
⇒ 4 điểm A,F,H,E cùng thuộc 1 đường tròn có tâm là trung điểm của AH
7 tháng 11 2021
a: Xét tứ giác BFEC có
\(\widehat{BEC}=\widehat{BFC}=90^0\)
Do đó: BFEC là tứ giác nội tiếp
hay B,F,E,C cùng thuộc 1 đường tròn