Lớp 7 A có 15 học sinh nữ và 25 học sinh nam. Chọn ra ngẫu nhiên một học sinh trong lớp. Tìm số phần tử của tập hợp E gồm các kết quả có thể xảy ra đối với học sinh được chọn ra. Sau đó, hãy tính xác suất của mỗi biến cố sau: a) “Học sinh được chọn ra là học sinh nữ”; b) “Học sinh được chọn ra là học sinh nam”;
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tập hợp E gồm các kết quả có thể xảy ra đối với số tự nhiên được viết ra là:
E = {Ánh; Châu; Hương; Hoa; Ngân; Bình; Dũng; Hùng; Huy; Việt}
Số phần tử của E là 10
a) Có năm kết quả thuận lợi cho biến cố “Học sinh được chọn ra là học sinh nữ” là: Ánh, Châu, Hương, Hoa, Ngân.
Vì thế, xác suất của biến cố trên là: \(\dfrac{5}{{10}} = \dfrac{1}{2}\)
b) Có năm kết quả thuận lợi cho biến cố “Học sinh được chọn ra là học sinh nam” là: Bình, Dũng, Hùng, Huy, Việt.
Vì thế, xác suất của biến cố trên là: \(\dfrac{5}{{10}} = \dfrac{1}{2}\)

a) Tập hợp P gồm các kết quả có thể xảy ra đối với học sinh được chọn ra là:
P = {Ánh, Châu, Hương, Hoa, Ngân, Bình, Dũng, Hùng, Huy, Việt}
b) Trong 10 bạn ở Tổ I của lớp 7D, có 5 học sinh nữ là: Ánh, Châu, Hương, Hoa, Ngân.
Vậy có năm kết quả thuận lợi cho biến cố “Học sinh được chọn ra là học sinh nữ” là: Ánh, Châu, Hương, Hoa, Ngân (lấy ra từ tập hợp P = {Ánh, Châu, Hương, Hoa, Ngân, Bình, Dũng, Hùng, Huy, Việt}).
c) Trong 10 bạn ở Tổ I của lớp 7D, có 5 học sinh nam là: Bình, Dũng, Hùng, Huy, Việt.
Vậy có năm kết quả thuận lợi cho biến cố “Học sinh được chọn ra là học sinh nam” là: Bình, Dũng, Hùng, Huy, Việt (lấy ra từ tập hợp P = {Ánh, Châu, Hương, Hoa, Ngân, Bình, Dũng, Hùng, Huy, Việt}).

tham khảo
a) Số kết quả thuận lợi cho biến cố A là \(C^3_{17}=680\)
Số kết quả thuận lợi cho biến cố B là \(C^2_{17}.C^1_{15}=2040\)
b)\(A\cup B\) là biến cố "Có ít nhất 2 học sinh nữ trong 3 học sinh được chọn"Số kết quả thuận lợi cho biến cố \(A\cup B\) là:\(680+2040=2720\)
Đáp án B
Gọi x,y lần lượt là số học sinh nữ ở nhóm I và nhóm II. Khi đó số học sinh nam ở nhóm II là 25 − 9 + x − y = 16 − x − y . Điều kiện để mỗi nhóm đều có học sinh nam và nữ là x ≥ 1, y ≥ 1,16 − x − y ≥ 1 ; x , y ∈ ℕ .
Xác suất để chọn ra được hai học sinh nam bằng C 9 1 C 16 − x − y 1 C 9 + x 1 C 16 − x 1 = 0,54
⇔ 9 16 − x − y 9 + x 16 − x = 0,54 ⇔ 144 − 9 x − 9 y 144 + 7 x − x 2 = 0,54 ⇔ y = 184 25 − 71 50 x + 3 50 x 2
Ta có hệ điều kiện sau x ≥ 1 184 25 − 71 50 x + 3 50 x 2 ≥ 1 16 − x − 184 25 − 71 50 x + 3 50 x 2 ≥ 1 x ∈ ℕ
⇔ x ≥ 1 3 50 x 2 − 71 50 x + 159 25 ≥ 0 − 3 50 x 2 + 21 50 x + 191 25 ≥ 0 x ∈ ℕ ⇔ x ≥ 1 x ≥ 53 3 x ≤ 6 21 − 5 201 6 ≤ x ≤ 21 + 5 201 6 x ∈ ℕ ⇔ 1 ≤ x ≤ 6 x ∈ ℕ
Ta có bảng các giá trị của :
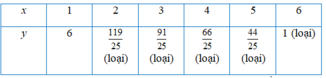
Vậy ta tìm được hai cặp nghiệm nguyên x ; y thỏa mãn điều kiện là 1 ; 6 và 6 ; 1 .
Xác suất để chọn ra hai học sinh nữ là C x 1 C y 1 C 9 + x 1 C 16 − x 1 = x y 9 + x 16 − x .
Nếu x ; y ∈ 1 ; 6 , 6 ; 1 thì xác suất này bằng 1 25 = 0,04 .

\(\Omega \) là tập tất cả 6 học sinh trong 12 học sinh. Vậy \(n\left( \Omega \right) = C_{12}^6 = 924\).
Gọi C là biến cố: “Có 3 học sinh nam và 3 học sinh nữ”. Có \(C_7^3\) cách chọn chọn 3 học sinh nam và \(C_5^3\) cách chọn 3 học sinh nữ. Theo quy tắc nhân, ta có \(C_7^3.C_5^3 = 350\) cách chọn 3 học sinh nam và 3 học sinh nữ tức là \(n\left( C \right) = 350\).Vậy \(P\left( C \right) = \frac{{350}}{{924}} \approx 0,3788\).

Đáp án C.
Phương pháp:
Xác suất của biến cố A:
P A = n A n Ω .
Cách giải:
Số phần tử của không gian mẫu:
n Ω = C 9 3
A: “Số học sinh nam nhiều hơn số học sinh nữ”
Ta có 2 trường hợp:
+) Chọn ra 2 nam, 1 nữ:
+) Chọn ra 3 nam, 0 nữ.
⇒ n A = C 5 2 C 4 1 + C 5 3
⇒ P A = n A n Ω = C 5 2 C 4 1 + C 5 3 C 9 3 = 25 42

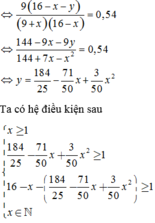
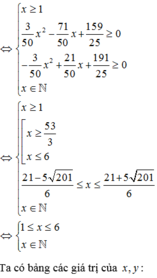


cứu
a: n(E)=40
A là biến cố "học sinh được chọn ra là nữ"
n(A)=15
=>P(A)=15/40=3/8
b: biến cố học sinh được chọn ra là nam là biến cố đối của biến cố học sinh được chọn ra là nữ
=>P=1-3/8=5/8