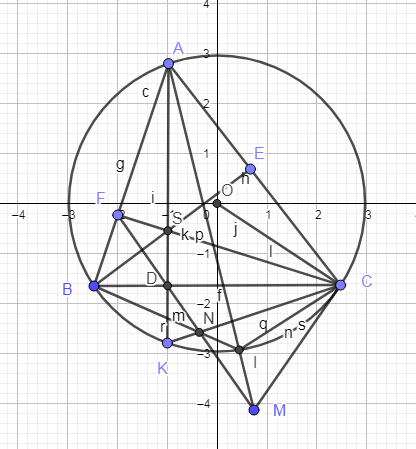
cho tam giác ABC có ba góc nhọn (AB∠AC) nội tiếp đường tròn (o) vẽ tiếp tuyến tại A của đường tròn(o) cắt đường thẳng BC tại S tia phân giác của góc BAC cắt BC tại K và cắt đường tròn (o) tại E ,OE cắ...

K

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

TH

Trần hữu tráng

15 tháng 3 2023

cho tam giác ABC có ba góc nhọn (AB∠AC) nội tiếp đường tròn (o) vẽ tiếp tuyến tại A của đường tròn(o) cắt đường thẳng BC tại S tia phân giác của góc BAC cắt BC tại K và cắt đường tròn (o) tại E ,OE cắt dây BC tại I a/ chứng minh:SA2 =SB*SC b/chứng minh:OE⊥BC tại I d/vẽ tiếp tuyến SD của đường tròn (o) D là tiếp điểm D khác A . chứng minh:tứ giác SAOD nội tiếp được đường tròn và I...

1

NL

Nguyễn Lê Phước Thịnh

15 tháng 3 2023

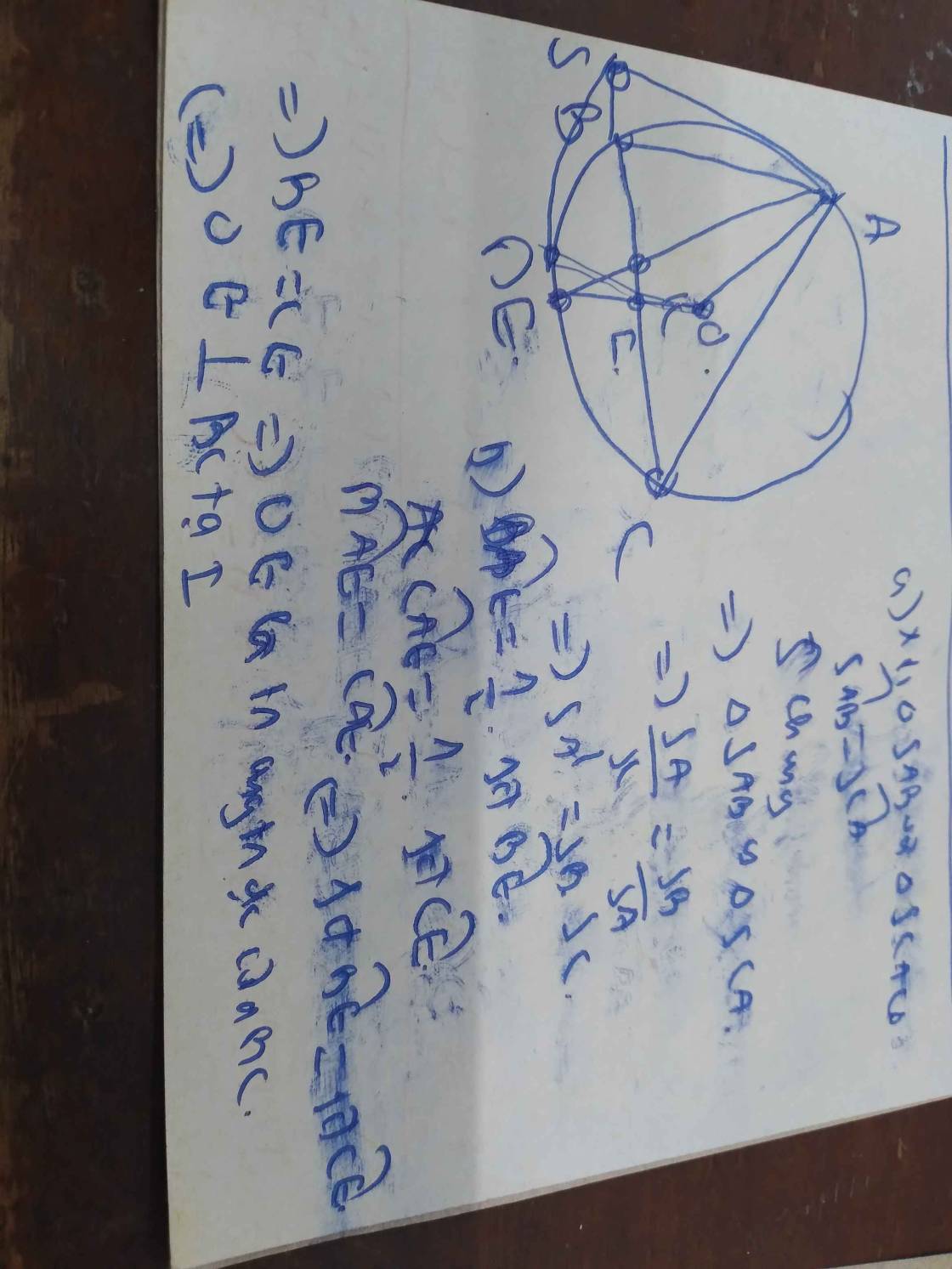
loading...

Những câu hỏi liên quan

PD

phúc du nguyễn

12 tháng 5 2020 - olm

cho tam giác ABC có ba góc nhọn (AB∠AC) nội tiếp đường tròn (o) vẽ tiếp tuyến tại A của đường tròn(o) cắt đường thẳng BC tại S tia phân giác của góc BAC cắt BC tại K và cắt đường tròn (o) tại E ,OE cắt dây BC tại Ia/ chứng minh:SA2 =SB*SCb/chứng minh:OE⊥BC tại Id/vẽ tiếp tuyến SD của đường tròn (o) D là tiếp điểm D khác A . chứng minh:tứ giác SAOD nội tiếp được đường tròn và I thuộc...

0

BK

bảo khang

15 tháng 3 2023 - olm

CHo tam giác ABC có 3 góc nhọn, AB < AC nội tiếp đường tròn (O). Tiếp tuyến tại A của đường tròn (O) cắt đường thẳng BC tại S a) Chứng minh SA2 = SB.SC b) Tia phân giác của BAC cắt dây và cung nhỏ BC tại D và E. Chứng minh: SA = SD c) Vẽ đường cao AH của tam giác ABC. CHứng tỏ: OE vuông góc BC và AE là tia phân giác của góc...

1

BK

bảo khang

15 tháng 3 2023

giúp em đi ạ

TV

Tường Vân

7 tháng 2 2021

5/ Cho AABC có ba góc nhọn nội tiếp đường tròn (O) (AB < AC). Vẽ đường cao AD của tân giác ABC. Tia phân giác của BAC cắt BC tại K và cắt (O) tai E. a) Chúng minh AD // OE b) Tiếp tuyến tại A của đường tròn (O) cắt tia CB tại M. Cm: MA2= MB.MC c) Chúng minh MA = MK. d) Vē đường kính EF và tiếp tuyến MI của đường tròn (O) (I khác A và I là tiếp diểm). Chúng minh F, K, I thång hàng.

0

VA

Văn A Lê

19 tháng 3 2023

Cho tam giác ABC nhọn (AB AC) nội tiếp đường tròn (O). Tiếp tuyến tại A của đường tròn (O) cắt đường thẳng BC tại D. Vẽ OM vuông góc với BC tại M. a) Chứng minh tứ giác AOMD nội tiếp. b) Tia OM cắt đường tròn (O) tại điểm N, AN và BC cắt nhau tại I. Chứng minh AN là tia phân giác của góc BAC và AD=DI c) Tia phân giác của ABC cắt AN tại H. Giả sử dây AB cố định và điểm C di chuyển trên...

1

NL

Nguyễn Lê Phước Thịnh

21 tháng 3 2023

a: góc OAD+góc OMD=180 độ

=>OADM nội tiếp

b: ΔOBC cân tại O

mà ON là đường cao

nên ONlà trung trực của BC

=>sđ cung NB=sd cung NC

=>góc BAN=góc CAN

=>AN là phân giác của góc BAC

góc DAI=1/2*sđ cung AN

góc DIA=1/2(sđ cung AB+sđ cung NC)

=1/2(sđ cung AB+sđ cung NB)

=1/2*sđ cung AN

=>góc DAI=góc DIA

=>ΔDAI cân tại D

NT

nguyễn thu hiếu

2 tháng 5 2016 - olm

cho tam giác ABC có ba góc nhọn (AB<AC) nội tiếp đương tron (O) .vẽ tiếp tuyến tai A của đường tron (O) cắt đường thẳng BC tại S . Tia phân giác của góc BAC cắt BC tai K và cắt đường tròn (O) tại E ,OE cắt dây BC tại \(I\)A) chứng minh \(SA^2=SB.SC\)B)chứng minh OE vuông góc BCtại \(I\)c ) chứng minh \(SA=SK\)D) Vẽ tiếp tuyến SD của đường tròn tâm (O) ( Dlá tiếp điểm ,Dkhác A ). Chứng minh tư giác SAOD...

0

T

Tâm

23 tháng 5 2021

Cho tam giác ABC có 3 góc nhọn, AB < AC và nội tiếp đường tròn (O). Ba đường cao AD, BE, CF cắt nhau tại H. Tia AD cắt đường tròn (O) ở K( K khác A). Tiếp tuyến tại C của đường tròn (O) cắt đường thẳng FD tại M.a) Chứng minh tứ giác ACDF nội tiếpb) AM cắt đường tròn (O) tại I( I khác A). Chứng minh MC2 = MI. MA và tam giác CMD cân.c) MD cắt BI tại N. Chứng minh 3 điểm C, K, N thẳng hàng.Giúp mình với...

0

TN

ᴾᴿᴼシ๖ۣۜT๖ۣۜH๖ۣۜN ๖ۣۜN๖ۣۜG ๖ۣۜH๖ۣۜC...

23 tháng 5 2021

Cho tam giác ABC có 3 góc nhọn, AB < AC và nội tiếp đường tròn (O). Ba đường cao AD, BE, CF cắt nhau tại H. Tia AD cắt đường tròn (O) ở K( K khác A). Tiếp tuyến tại C của đường tròn (O) cắt đường thẳng FD tại M.a) Chứng minh tứ giác ACDF nội tiếpb) AM cắt đường tròn (O) tại I( I khác A). Chứng minh MC2 = MI. MA và tam giác CMD cân.c) MD cắt BI tại N. Chứng minh 3 điểm C, K, N thẳng hàng.Giúp mình với...

#Toán lớp 12

0

TD

Trần Đức Huy

5 tháng 2 2022

Cho tam giác ABC có 3 góc nhọn, AB < AC và nội tiếp đường tròn (O). Ba đường cao AD, BE, CF cắt nhau tại H. Tia AD cắt đường tròn (O) ở K( K khác A). Tiếp tuyến tại C của đường tròn (O) cắt đường thẳng FD tại M. AM cắt đường tròn (O) tại I( I khác A). MD cắt BI tại N. Chứng minh góc MDI = góc MCICần gấp!!!!! Ai giúp...

1

NV

Nguyễn Việt Lâm

Giáo viên

5 tháng 2 2022

Hai góc này không bằng nhau thì chứng minh làm sao được em?

Em thử sử dụng tính năng đo góc của geogebra là biết.

TD

Trần Đức Huy

4 tháng 2 2022

Cho tam giác ABC có 3 góc nhọn, AB < AC và nội tiếp đường tròn (O). Ba đường cao AD, BE, CF cắt nhau tại H. Tia AD cắt đường tròn (O) ở K( K khác A). Tiếp tuyến tại C của đường tròn (O) cắt đường thẳng FD tại M. AM cắt đường tròn (O) tại I( I khác A). MD cắt BI tại N. Chứng minh 3 điểm C, K, N thẳng hàng.giúp gấp...

1

DT

Đỗ Tuệ Lâm

4 tháng 2 2022

ta có: \(MC^2=MI.MA\)

\(\Rightarrow MD^2=MI.MA\) ( do tam giác MCD cân tại M)

\(\Rightarrow\dfrac{MD}{MA}=\dfrac{ MI}{MD}\)

Xét tam giác MDI và tam giác MAD có :

\(\left\{{}\begin{matrix}DMAgócchung\\\dfrac{MD}{MA}=\dfrac{MI}{MD}\end{matrix}\right.\)

=> tam giác MDI đồng dạng tam giác MAD ( g -c)

=> góc MDI = góc MAD (1)

tứ giác DNIC nội tiếp => góc MDI = góc MCI (2)

từ 1 và 2 suy ra :góc NCI = góc HAD

mà góc MAD = góc KCI

=> góc NCI = góc KCI

vậy 3 điểm C ; K ; N thẳng hàng ( đpcm)