Giải pt 15 - 7x = 9-3xg.x-3=18 Mọi người giúp em với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(1,\dfrac{3x+2}{6}-\dfrac{3x-2}{4}=\dfrac{15}{8}\\ \Leftrightarrow\dfrac{4\left(3x+2\right)}{24}-\dfrac{6\left(3x-2\right)}{24}-\dfrac{45}{24}=0\\ \Leftrightarrow12x+24-18x+12-45=0\\ \Leftrightarrow-6x-9=0\\ \Leftrightarrow x=-\dfrac{3}{2}\)
2, ĐKXĐ:\(x\ne\pm3\)
\(\dfrac{x+2}{3+x}-\dfrac{x}{3-x}=\dfrac{8x-6}{9-x^2}\\ \Leftrightarrow\dfrac{\left(x+2\right)\left(3-x\right)}{\left(3+x\right)\left(3-x\right)}-\dfrac{x\left(3+x\right)}{\left(3+x\right)\left(3-x\right)}-\dfrac{8x-6}{\left(3+x\right)\left(3-x\right)}=0\\ \Leftrightarrow\dfrac{-x^2+x+6-3x-x^2-8x+6}{\left(3+x\right)\left(3-x\right)}=0\\ \Leftrightarrow-2x^2-10x+12=0\\ \Leftrightarrow x^2+5x-6=0\\ \Leftrightarrow\left(x-1\right)\left(x+6\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=1\left(tm\right)\\x=-6\left(tm\right)\end{matrix}\right.\)
\(a,\dfrac{3x+2}{6}-\dfrac{3x-2}{4}=\dfrac{15}{8}\)
\(\Leftrightarrow4\left(3x+2\right)-6\left(3x-2\right)=45\)
\(\Leftrightarrow12x+8-18x+12=45\)
\(\Leftrightarrow12x-18x=45-12-8\)
\(\Leftrightarrow-6x=25\)
\(\Leftrightarrow x=\dfrac{-25}{6}\)
Vậy \(S=\left\{\dfrac{-25}{6}\right\}\)
\(b,\dfrac{x+2}{3+x}-\dfrac{x}{3-x}=\dfrac{8x-6}{9-x^2}\left(ĐKXĐ:x\ne3;x\ne-3\right)\)
\(\Leftrightarrow\left(x+2\right)\left(3-x\right)-x\left(3+x\right)=8x-6\)
\(\Leftrightarrow3x-x^2+6-2x-3x-x^2=8x-6\)
\(\Leftrightarrow-x^2-x^2+3x-2x-3x-8x=-6+6\)
\(\Leftrightarrow-2x^2-10x=0\)
\(\Leftrightarrow-2x\left(x-5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}-2x=0\\x-5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\left(nhận\right)\\x=5\left(nhận\right)\end{matrix}\right.\)
Vậy \(S=\left\{0;5\right\}\)

Nếu a = 18 , b = 6 và c=3 thì a x b : c = 18 x 6 : 3 = 108 : 3 = 36
nhớ k cho mình nha

Vì GTTĐ luôn lớn hơn hoặc bằng 0 với mọi x, do đó :
\(\left|x+1\right|+\left|2x+15\right|+\left|3x+6041\right|\ge0\forall x\)
\(\Leftrightarrow7x\ge0\)
\(\Leftrightarrow x\ge0\)
Từ điều kiện này của x ta có phương trình :
\(x+1+2x+15+3x+6041=7x\)
\(\Leftrightarrow6x+6057=7x\)
\(\Leftrightarrow7x-6x=6057\)
\(\Leftrightarrow x=6057\)
Vậy tập nghiệm của pt là S = { 6057 }

Trừ từng vế của 2 PT ta có:
\(x^3-y^3-\left(4x-4y\right)=0\Leftrightarrow\left(x-y\right)\left(x^2+xy+y^2\right)-4\left(x-y\right)=0\Leftrightarrow\left(x-y\right)\left(x^2+xy+y^2-4\right)=0\)

=> 72 - 20x - 36x - 84 = 30x - 240 - 6x + 84
=> (72 - 84 ) - (20x + 36x ) = (30x - 6x ) - 240 + 84
=> -12 - 56x = 24x - 156
=> -12 + 156 = 24x + 56x
=> 144 = 80x
=> x = 144 : 80
=> x = 9/5

TH1: \(m=-1\) thỏa mãn (dễ dàng kiểm tra các giá trị \(f\left(-1\right)>0\) ; \(f\left(0\right)< 0\) ; \(f\left(3\right)>0\) nên pt có ít nhất 2 nghiệm thuộc (-1;0) và (0;3)
TH2: \(m>-1\):
\(\lim\limits_{x\rightarrow+\infty}f\left(x\right)=\lim\limits_{x\rightarrow+\infty}x^4\left[m\left(1-\dfrac{2}{x}\right)^2\left(1+\dfrac{9}{x}\right)+1-\dfrac{32}{x^4}\right]=+\infty.\left(m+1\right)=+\infty>0\)
\(\Rightarrow\) Luôn tồn tại 1 giá trị \(x=a\) đủ lớn sao cho \(f\left(a\right)>0\)
\(f\left(0\right)=-32< 0\Rightarrow f\left(a\right).f\left(0\right)< 0\)
\(\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm dương
\(f\left(-9\right)=9^4-32>0\Rightarrow f\left(-9\right).f\left(0\right)< 0\)
\(\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm âm thuộc \(\left(-9;0\right)\)
\(\Rightarrow f\left(x\right)\) luôn có ít nhất 2 nghiệm
TH3: \(m< -1\) tương tự ta có: \(\lim\limits_{x\rightarrow+\infty}f\left(x\right)=\lim\limits_{x\rightarrow-\infty}=+\infty.\left(m+1\right)=-\infty\)
\(\Rightarrow\) Luôn tồn tại 1 giá trị \(x=a>0\) đủ lớn và \(x=b< 0\) đủ nhỏ sao cho \(\left\{{}\begin{matrix}f\left(a\right)< 0\\f\left(b\right)< 0\end{matrix}\right.\)
Lại có \(f\left(-9\right)=9^4-32>0\) \(\Rightarrow\left\{{}\begin{matrix}f\left(-9\right).f\left(a\right)< 0\\f\left(-9\right).f\left(b\right)< 0\end{matrix}\right.\)
\(\Rightarrow\) Pt luôn có ít nhất 2 nghiệm thuộc \(\left(-\infty;-9\right)\) và \(\left(-9;+\infty\right)\)
Vậy pt luôn có ít nhất 2 nghiệm với mọi m

a) \(\dfrac{3}{8}+\dfrac{15}{-25}+\dfrac{3}{5}\)
\(=\dfrac{-9}{40}+\dfrac{3}{5}\)
\(=\dfrac{3}{8}\)
b) \(\dfrac{-5}{18}+\dfrac{23}{45}-\dfrac{9}{10}\)
\(=\dfrac{7}{30}-\dfrac{9}{10}\)
\(=\dfrac{-2}{3}\)
c) \(\dfrac{-5}{12}+\dfrac{15}{18}-2,25\)
\(=\dfrac{5}{12}-2,25\)
\(=\dfrac{-11}{6}\)
d) \(\dfrac{5}{6}+\dfrac{2}{3}-0,5\)
\(=\dfrac{3}{2}-0,5\)
\(=1\)
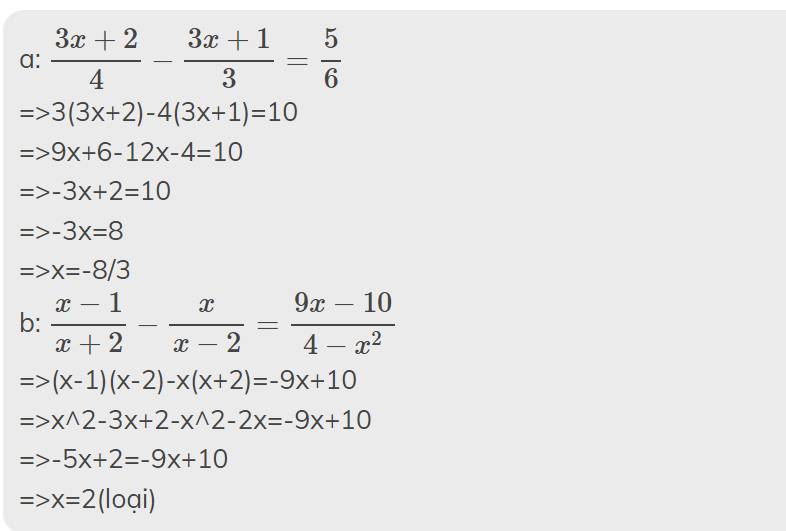
Em em đề có lỗi ở đâu không nhỉ?