Lim Un = 1 + 2 + 3 +...+ n/ n2 + 1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
14 tháng 9 2018
Ta có: u n = n 2 + 1 − n = n 2 + 1 − n n 2 + 1 + n n 2 + 1 + n = 1 n 1 + 1 n 2 + 1 = 1 n . 1 1 + 1 n 2 + 1
Vì lim 1 n = 0 , lim 1 1 + 1 n 2 + 1 = 1 2 nên lim u n = 0 .
Chọn đáp án A.
CM
5 tháng 7 2018
Ta có:
lim u n = lim n − 1 2 n + 2 n 4 + n 2 − 1 = lim n − 1 2 2 n + 2 n 4 + n 2 − 1 = lim u n = lim n − 1 2 n + 2 n 4 + n 2 − 1 = lim 2 n − 2 n 2 − 2 n 3 + 2 n 4 1 + 1 n 2 − 1 n 4 = 0.
Chọn đáp án B
CM
12 tháng 10 2018
Đáp án là B
Ta có: l i m u n = l i m n - 1 2 n + 2 n 4 + n 2 - 1
=
l
i
m
n
-
1
2
2
n
+
2
n
4
+
n
2
-
1
=
l
i
m
2
n
3
-
2
n
2
-
2
n
+
2
n
4
+
n
2
-
1
= l i m 2 n - 2 n 2 - 2 n 3 + 2 n 4 1 + 1 n 2 - 1 n 4 = 0
CM
4 tháng 12 2019
Đáp án là D.
Ta có
f n = n 2 + 1 + n 2 + 1 = n 2 + 1 2 + 2 n . n 2 + 1 + n 2 + 1 = n 2 + 1 n 2 + 1 + 2 n + 1
= n 2 + 1 n + 1 2 + 1
Do đó: f 2 n − 1 f 2 n = 2 n − 1 2 + 1 2 n 2 + 1 2 n 2 + 1 2 n + 1 2 + 1 = 2 n − 1 2 + 1 2 n + 1 2 + 1
Suy ra
u n = f 1 . f 3 . f 5 ... f 2 n − 1 f 2 . f 4 . f 6 ... f 2 n = f 1 f 2 ⋅ f 3 f 4 ⋅ f 5 f 6 ⋅ ⋅ ⋅ f 2 n − 1 f 2 n
= 1 2 + 1 3 2 + 1 ⋅ 3 2 + 1 5 2 + 1 ⋅ 5 2 + 1 7 2 + 1 ⋅ ⋅ ⋅ 2 n − 1 2 + 1 2 n + 1 2 + 1 = 2 2 n + 1 2 + 1 = 1 2 n 2 + 2 n + 1
⇒ n u n = n . 1 2 n 2 + 2 n + 1
⇒ lim n u n = 1 2
CM
29 tháng 9 2019
Ta có: u n = n + n 2 + 1 n .3 n = n + n 2 + 1 n n .3 n n = 1 + 1 + 1 n 2 3 n = 1 3 n 1 + 1 + 1 n 2
Vì lim 1 n 2 = 0 nên lim 1 + 1 + 1 n n = 2 và lim 1 3 n = 0.
Do đó lim u n = 0
Chọn đáp án D
CM
7 tháng 11 2019
Chia cả tử và mẫu của phân thức cho n 3 ( n 3 là lũy thừa bậc cao nhất của n trong phân thức), ta được:
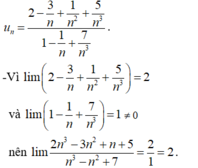
Chọn C.
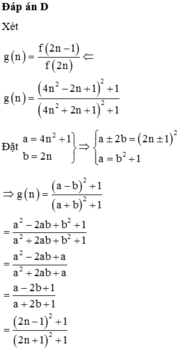
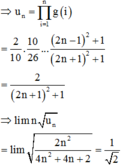
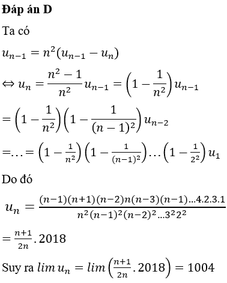
\(=lim\left(\dfrac{n^2+n}{2n^2+2}\right)\)
\(=\lim\limits\dfrac{1+\dfrac{1}{n}}{2+\dfrac{1}{n^2}}=\dfrac{1}{2}\)