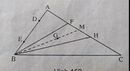
: Cho tam giác ABC. Trên cạnh AB lấy hai điểm D và E sao cho AD = BE. Trên cạnh AC lấy hai điểm F và H sao cho AF = CH. Chứng minh rằng các tam giác BFH và CDE có cùng một trọng tâm.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

TT
Thang Thanh Thảo
9 tháng 2 2021
Bạn tham khảo ak

Đúng(0)
Những câu hỏi liên quan

13 tháng 4 2017
hình chắc bn vẽ đc
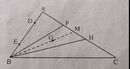
xét tg AIB và CIE có
AB=CE(gt)
AI=CI(I thuộc trug trực AC)
BI=EI(I thuộc trug trực BE)
suy ra tg AIB= CIE(đ p c m)
b) xét tg AIC có AI= IC (cmt)
suy ra tg AIC cân tại I
suy ra góc IAC= góc ACI
mà góc ACI= góc IAB
suy ra góc IAB =góc IAC
suy ra AI là pg góc BAC
tick mk nhaaaaaaaaaaaaaaaaaaaaa

11 tháng 8 2021
a: Xét ΔAEB và ΔADC có
AE=AD
\(\widehat{DAC}\) chung
AB=AC
Do đó: ΔAEB=ΔADC
Suy ra: BE=CF
b: Ta có: AD+DB=AB
AE+EC=AC
mà AD=AE
và AB=AC
nên DB=EC
Xét ΔDBC và ΔECB có
DB=EC
\(\widehat{DBC}=\widehat{ECB}\)
BC chung
Do đó: ΔDBC=ΔECB
Suy ra: \(\widehat{ODB}=\widehat{OEC}\)
Xét ΔODB và ΔOEC có
\(\widehat{ODB}=\widehat{OEC}\)
BD=EC
\(\widehat{DBO}=\widehat{ECO}\)
Do đó: ΔODB=ΔOEC