Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
`a)`
`BD` là p/g `hat(ABC)=>hat(B_1)=hat(B_2)`
Xét `Delta BAD` và `Delta BED` có :
`{:(hat(BAD)=hat(BED)(=90^0)),(BD-chung),(hat(B_1)=hat(B_2)(cmt)):}}`
`=>Delta BAD=Delta BED(c.h-g.n)(đpcm)`
`b)`
Có `Delta BAD=Delta BED(cmt)=>AD=ED`
Xét `Delta ADF` và `Delta EDC` có :
`{:(hat(A_1)=hat(E_1)(=90^0)),(AD=ED(cmt)),(hat(D_1)=hat(D_2)(đối.đỉnh)):}}`
`=>Delta ADF=Delta EDC(c.h-g.n)`
`=>AF=EC` (2 cạnh t/ứng )
mà `AB=BE(Delta BAD=Delta BED)`
nên `AB+AF=BE+EC`
hay `BF=BC`
`=>Delta BFC` cân tại `B(đpcm)`
`c)`
+,Có `Delta ABE` cân tại `B(AB=BE)=>hat(A_2)=(180^0-hat(BAE))/2`
hay `hat(A_2)=(180^0-hat(FBC))/2` (1)
`Delta BFC` cân tại `B(cmt)=>hat(BFC)=(180^0-hat(FBC))/2`(2)
Từ (1) và (2) `=>AF////FC` `(**)`
+, Có `AB=BE(cmt)=>B in `trung trực `AE` (3)
`AD=ED(cmt)=>D in` trung trực `AE` (4)
Từ (3);(4) `=>BD` là trung trực `AE`
`=>BD ⊥ AE` `(** **)`
+,Từ `(**)` và `(** **)=>BD⊥FC(đpcm)`
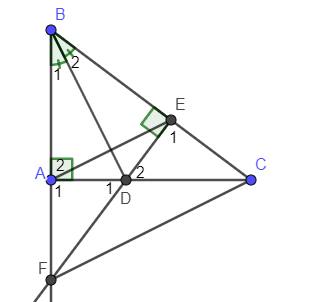
a; Xét ΔBAD vuôg tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
b: Xét ΔBEF vuông tại E và ΔBAC vuông tại A có
BE=BA
góc B chung
=>ΔBEF=ΔBAC
=>BF=BC
c: ΔCBF cân tại B
mà BD là phân giác
nên BD là trung tuyến
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
b: Xét ΔBEF vuông tại E và ΔBAC vuông tại A có
BE=BA
góc EBF chung
=>ΔBEF=ΔBAC
=>BF=BC
c: ΔBFC can tai B
mà BD là phân giác
nên BD là trung tuyến
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
b: ΔBAD=ΔBED
=>DA=DE
Xét ΔDAF vuông tại A và ΔDEC vuông tại E có
DA=DE
\(\widehat{ADF}=\widehat{EDC}\)
=>ΔDAF=ΔDEC
=>DF=DC
=>ΔDFC cân tại D
c: Xét ΔBFC có
FE,CAlà đường cao
FE cắt CA tại D
=>D là trực tâm
=>BD vuông góc CF tại H
=>DH vuông góc CF tại H
mà ΔDFC cân tại D
nên H là trung điểm của FC
Xét ΔKFC có
CD là trung tuyến
CI=2/3CD
Do đó: I là trọng tâm
mà H là trung điểm của CF
nên K,I,H thẳng hàng
a) Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
Do đó: ΔABD=ΔEBD(Cạnh huyền-góc nhọn)
Suy ra: AB=BE(hai cạnh tương ứng)
b) Ta có: ΔABD=ΔEBD(cmt)
nên DA=DE(hai cạnh tương ứng)
Xét ΔADF vuông tại A và ΔEDC vuông tại E có
DA=DE(cmt)
\(\widehat{ADF}=\widehat{EDC}\)(hai góc đối đỉnh)
Do đó: ΔADF=ΔEDC(cạnh góc vuông-góc nhọn kề)
Suy ra: DF=DC(hai cạnh tương ứng)
Xét ΔDFC có DF=DC(cmt)
nên ΔDFC cân tại D(Định nghĩa tam giác cân)
c) Ta có: ΔADF=ΔEDC(cmt)
nên AF=EC(Hai cạnh tương ứng)
Ta có: BA+AF=BF(A nằm giữa B và F)
BE+EC=BC(E nằm giữa B và C)
mà BA=BE(cmt)
và AF=EC(Cmt)
nên BF=BC
Xét ΔBAE có BA=BE(cmt)
nên ΔBAE cân tại B(Định nghĩa tam giác cân)
Ta có: ΔBAE cân tại B(cmt)
nên \(\widehat{BAE}=\dfrac{180^0-\widehat{B}}{2}\)(Số đo của một góc ở đáy trong ΔBAE cân tại B)(1)
Xét ΔBFC có BF=BC(cmt)
nên ΔBFC cân tại B(Định nghĩa tam giác cân)
Ta có: ΔBFC cân tại B(cmt)
nên \(\widehat{BFC}=\dfrac{180^0-\widehat{B}}{2}\)(Số đo của một góc ở đáy trong ΔBFC cân tại B)(2)
Từ (1) và (2) suy ra \(\widehat{BAE}=\widehat{BFC}\)
mà \(\widehat{BAE}\) và \(\widehat{BFC}\) là hai góc ở vị trí đồng vị
nên AE//FC(Dấu hiệu nhận biết hai đường thẳng song song)
a) Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
Do đó: ΔABD=ΔEBD(cạnh huyền-góc nhọn)
b) Ta có: ΔABD=ΔEBD(cmt)
nên BA=BE(Hai cạnh tương ứng)
Xét ΔABE có BA=BE(cmt)
nên ΔBAE cân tại B(Định nghĩa tam giác cân)
c) Ta có: ΔABD=ΔEBD(cmt)
nên DA=DE(hai cạnh tương ứng)
Xét ΔADF vuông tại A và ΔEDC vuông tại E có
DA=DE(cmt)
\(\widehat{ADF}=\widehat{EDC}\)(hai góc đối đỉnh)
Do đó: ΔADF=ΔEDC(cạnh góc vuông-góc nhọn kề)
Suy ra: DF=DC(hai cạnh tương ứng)
a; Xét ΔBAD vuôg tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
b: Xét ΔBEF vuông tại E và ΔBAC vuông tại A có
BE=BA
góc B chung
=>ΔBEF=ΔBAC
=>BF=BC
c: ΔCBF cân tại B
mà BD là phân giác
nên BD là trung tuyến