tính GTNN của P(x)
-5+x2+3x4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DH
3
16 tháng 1 2022
\(A\ge1\forall x\)
Dấu '=' xảy ra khi x=0
\(B\ge-5\forall x\)
Dấu '=' xảy ra khi x=0
LD
1
- 3x4 - x2 - 4x3
ABC cân tại A; AM là đường trung tuyến; BI là đường cao. AM cắt BI tại H, CH cắt AB tại D. 
AB 
ABC vuông tại A, đường phân giác BK. Kẻ KI vuông góc với BC (I
BC)
IF
+ 10
AH
Akai Haruma
Giáo viên
1 tháng 5 2023
Bạn nên tách lẻ từng bài ra để được hỗ trợ tốt hơn, không nên đăng 1 loạt bài như thế này nhé.
12 tháng 5 2023
2:
a: P(x)=3x^2-4x-1
Q(x)=-3x^2-4x-2
b:F(x)=-3x^2-4x-2-3x^2+4x+1=-6x^2-1
Q(x)=3x^2-4x-1+3x^2+4x+2=6x^2+1
c: F(-2)=-6*4-1=-25
Q(3)=-27-12-2=-41
24 tháng 4 2022
a) A(x) = 2x3 + 5 + x2 - 3x - 5x3 - 4
= 2x3 - 5x3 + x2 - 3x + 5 - 4
= -3x3 + x2 - 3x + 1
B(x) = -3x4 - x3 + 2x2 + 2x + x4 - 4 - x2
= -3x4 + x4 - x3 + 2x2 - x2 + 2x - 4
= -2x4 - x3 + x2 + 2x - 4
b)
H(x) = A(x) - B(x)
H(x) = (-3x3 + x2 - 3x + 1) - (-2x4 - x3 + x2 + 2x - 4)
= -3x3 + x2 - 3x + 1 + 2x4 + x3 - x2 - 2x + 4
= 2x4 - 3x3 + x3 + x2 - x2 - 3x - 2x + 1 + 4
= 2x4 - 2x3 -5x + 5
H
3 tháng 5 2023
\(a,N\left(x\right)=x^2+3x^4-2x-x^2+2x^3=3x^4+2x^3+\left(x^2-x^2\right)-2x\\ =3x^4+2x^3-2x\\ P\left(x\right)=-8+5x-6x^3-4x+6=-6x^3+\left(5x-4x\right)+\left(-8+6\right)\\ =-6x^3+x-2\)
Bậc của N(x) là 4
Bậc của P(x) là 3
\(b,P\left(x\right)+N\left(x\right)=3x^4+2x^3-2x-6x^3+x-2\\ =3x^4+\left(2x^3-6x^3\right)+\left(-2x+x\right)-2\\ =3x^4-4x^3-x-2\)
\(c,B\left(x\right)=-2x^2\left(x^3-2x+5x^2-1\right)\\ =\left(-2x^2\right).x^3+\left(-2x^2\right).\left(-2x\right)+\left(-2x^2\right).5x^2+\left(-2x^2\right).\left(-1\right)\\ =-2x^5+4x^3-10x^4+2x^2\\ =-2x^5-10x^4+4x^3+2x^2\)
J
0
LG
6 tháng 5 2018
a) A = 3x\(^4\) + 5x\(^2\)y\(^2\) + 2y\(^4\) + 2y\(^2\)
Đặt x\(^2\) = a, y\(^2\) = b ( a, b ≥ 0 ) khí đó:
a + b = 2
A = 3x\(^4\) + 5x\(^2\)y\(^2\) + 2y\(^4\) + 2y\(^2\)
⇒A = 3a\(^2\) + 5ab + 2b\(^2\) + 2b
⇒A = ( 3a\(^2\) + 3ab ) + ( 2b\(^2\) + 2ab ) + 2b
⇒A = 3a( a + b ) + 2b( a + b ) + 2b
⇒A = ( a + b )( 3a + 2b ) + 2b
⇒A = 2( 3a + 2b ) + 2b
⇒A = 2( 2a + 2b ) + 2a + 2b
⇒A = 4( a + b ) + 2( a + b )
⇒A = 4 \(\times\) 2 + 2 \(\times\) 2
⇒A = 12
HH
9 tháng 5 2018
a) A = 3x4 + 5x2y2 + 2y4 + 2y2 = 3x2(x2 + y2) + 2y2(x2 + y2) +2y2
= 3x2.2 + 2y2.2 + 2y2 = 6x2 + 6y2 = 6(x2 + y2) = 6.2 = 12
b) Ta thấy x4 ≥ 0; x2 ≥ 0. => 3x4 + x2 + 2018 > 0 với mọi x
Vậy đa thức A(x) không có nghiệm.
c) Tìm được P(x) = -2x + 3
1 tháng 5 2019
a) \(P\left(x\right)=3x^3-x^2-2x^4+3+2x^3+x+3x^4-x^2-2x^4+3+2x^3+x+3x^4\)
\(=2x^4+7x^3-2x^2+2x+6\)
\(Q\left(x\right)=-x^4+x^2-4x^3-2+2x^2-x-x^3-x^4+x^2-4x^3-2+2x^2-x-x^3\)
\(=-2x^4-10x^3+6x^2-2x-4\)
b) \(P\left(x\right)+Q\left(x\right)=2x^4+7x^3-2x^2+2x+6-2x^4-10x^3+6x^2-2x-4\)
\(=-3x^3+4x^2+2\)
CM
8 tháng 1 2019
Ta có
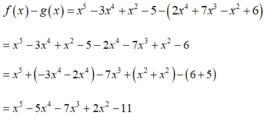
Sắp xếp theo lũy thừa tăng dần của biến ta được
- 11 + 2 x 2 - 7 x 3 - 5 x 4 + x 5
Chọn đáp án B
3x4+x2-5