cho △ABC có AB=4,8cm; BC3,6cm và AC=6,4cm. Trên cạnh AB lây điểm D sao cho AD=3,2cm và trên cạnh AC lấy điểm E sao cho AE2,4cm
a) C/m △AED ∼ △ABC
b) Tính DE
c) C/m góc ABC+góc DEC=180độ
d) F là giao điểm của ED và CB. C/m △FBD ∼ △FCE . Tính tỉ số đồng dạng
e) Tính FD,FB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
BH
1
28 tháng 10 2021
bn tự vẽ hình nha:3
Ta có: BC\(^2\) = 6\(^2\) = 36(1)
AB\(\)\(^2\) + AC\(^2\) = 3,6\(^2\) +\(4,8^2=36\) (2)
Từ (1) và (2) ⇒ \(BC^2=AB^2+AC^2\)
⇒ △ABC là tam giác vuông (định lý Pytago đảo)
Áp dụng tỉ số lượng giác vào △ABC, ta có:
sin B = \(\dfrac{AC}{BC}\) = \(\dfrac{4,8}{6}\) = \(\dfrac{4}{5}\) ⇒ góc B = 53 độ
⇒ góc C = 90 độ - 53 độ = 37 độ.
Áp dụng hệ thức lượng vào △ABC ⊥ A, đường cao AH, ta có:
AH.BC = AB.AC ⇒ AH = \(\dfrac{AB.AC}{BC}\)=\(\dfrac{3,6.4,8}{6}\)= 2,88 cm.
Vậy...(bn tự kết luận nha^^)
AH
Akai Haruma
Giáo viên
14 tháng 6 2023
Lời giải:
Áp dụng định lý Pitago:
$HC=\sqrt{AC^2-AH^2}=\sqrt{8^2-4,8^2}=6,4$ (cm)
Áp dụng hệ thức lượng trong tam giác vuông:
$BH.CH=AH^2$
$\Rightarrow BH=\frac{AH^2}{CH}=\frac{4,8^2}{6,4}=3,6$ (cm)
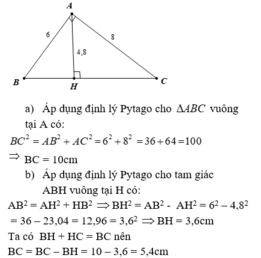
$BC=BH+CH=3,6+6,4=10$ (cm)
$AB=\sqrt{BC^2-AC^2}=\sqrt{10^2-8^2}=6$ (cm) - Theo định lý Pitago
1 tháng 3 2022
a.Áp dụng định lý pitago, ta có:
\(BC^2=AB^2+AC^2\)
\(\Rightarrow BC=\sqrt{6^2+8^2}=\sqrt{100}=10cm\)
b.AH: đã có
Áp dụng định lý pitago vào tam giác vuông AHC, có:
\(AC^2=AH^2+CH^2\)
\(\Rightarrow CH=\sqrt{AC^2-AH^2}=\sqrt{8^2-4,8^2}=\sqrt{40,96}=6,4cm\)
1 tháng 3 2022
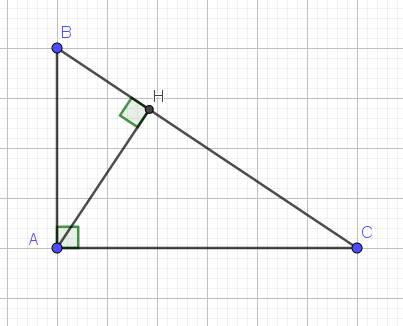
a: Xét ΔABC vuông tại A có
\(BC^2=AB^2+AC^2\)
nên BC=10(cm)
b: Xét ΔABH vuông tại H có \(AB^2=AH^2+HB^2\)
nên HB=3,6(cm)
=>HC=BC-HB=6,4(cm)
1 tháng 3 2022
câu này lúc nãy làm rồi em nhé! ( bổ sung BH )
Áp dụng định lý pitago vào tam giác vuông ABH, có:
\(AB^2=BH^2+AH^2\)
\(\Rightarrow BH=\sqrt{AB^2-AH^2}=\sqrt{6^2-4,8^2}=\sqrt{12,96}=3,6cm\)
27 tháng 9 2021
Xét ΔAHB vuông tại H có
\(AH^2+HB^2=AB^2\)
hay AH=3,6(cm)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(AB^2=BH\cdot BC\)
hay BC=7,5(cm)
Xét ΔABC vuông tại A có
\(BC^2=AB^2+AC^2\)
hay AC=4,5(cm)
NH
0
T
2
a: Xét ΔAED và ΔABC có
AE/AB=AD/AC
góc A chung
=>ΔAED đồng dạng vơi ΔABC
b: ΔAED đồng dạng vơi ΔABC
=>DE/BC=AE/AB
=>DE/3,6=2,4/4,8=1/2
=>DE=1,8cm
c: ΔAED đồng dạng với ΔABC
=>góc AED+góc ABC
=>góc DEC+góc DBC=180 dộ
d: Xét ΔFBD và ΔFEC có
góc FBD=góc FEC
góc F chung
=>ΔFBD đồng dạng vơi ΔFEC