Cho tam giác ABC.Từ điểm E trên cạnh AC kẻ ED //AB(D thuộcBC). KẺ EF //BC (F thuộc AB).Biết AE=BF. cm điểm D cách đều AB và AC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: EF // BD (gt)
BF // ED (gt)
Suy ra EF = BD; BF = DE (t/c đoạn chắn)
Trên AB lấy K sao cho AF = BK
\(\Delta AFE\) và \(\Delta KBD\) có:
AF = BK (cách vẽ)
AFE = KBD (đồng vị)
EF = BD (cmt)
Do đó, \(\Delta AFE=\Delta KBD\left(c.g.c\right)\)
=> AE = KD (2 cạnh t/ứ)
= BF = ED (theo gt AE = BF, theo cmt BF = ED)
Kẻ \(DM\perp AB;DN\perp AC\)
\(\Delta\) DMK vuông tại M và \(\Delta\) DNE vuông tại N có:
DK = DE (cmt)
MKD = NED (cùng đồng vị với FAE)
Do đó, \(\Delta DMK=\Delta DNE\) (cạnh huyền - góc nhọn)
=> DM = DN (2 cạnh t/ứ)
=> D cách đều AB và AC (đpcm)

a: Xét ΔABC và ΔAED có
AB/AE=AC/AD
góc A chung
=>ΔABC đồng dạng vơi ΔAED
b: EF//AB
=>EF/AB=CE/CA
=>EF/18=5/8
=>EF=90/8=11,25(cm)
BF/FC=AE/EC=3/5

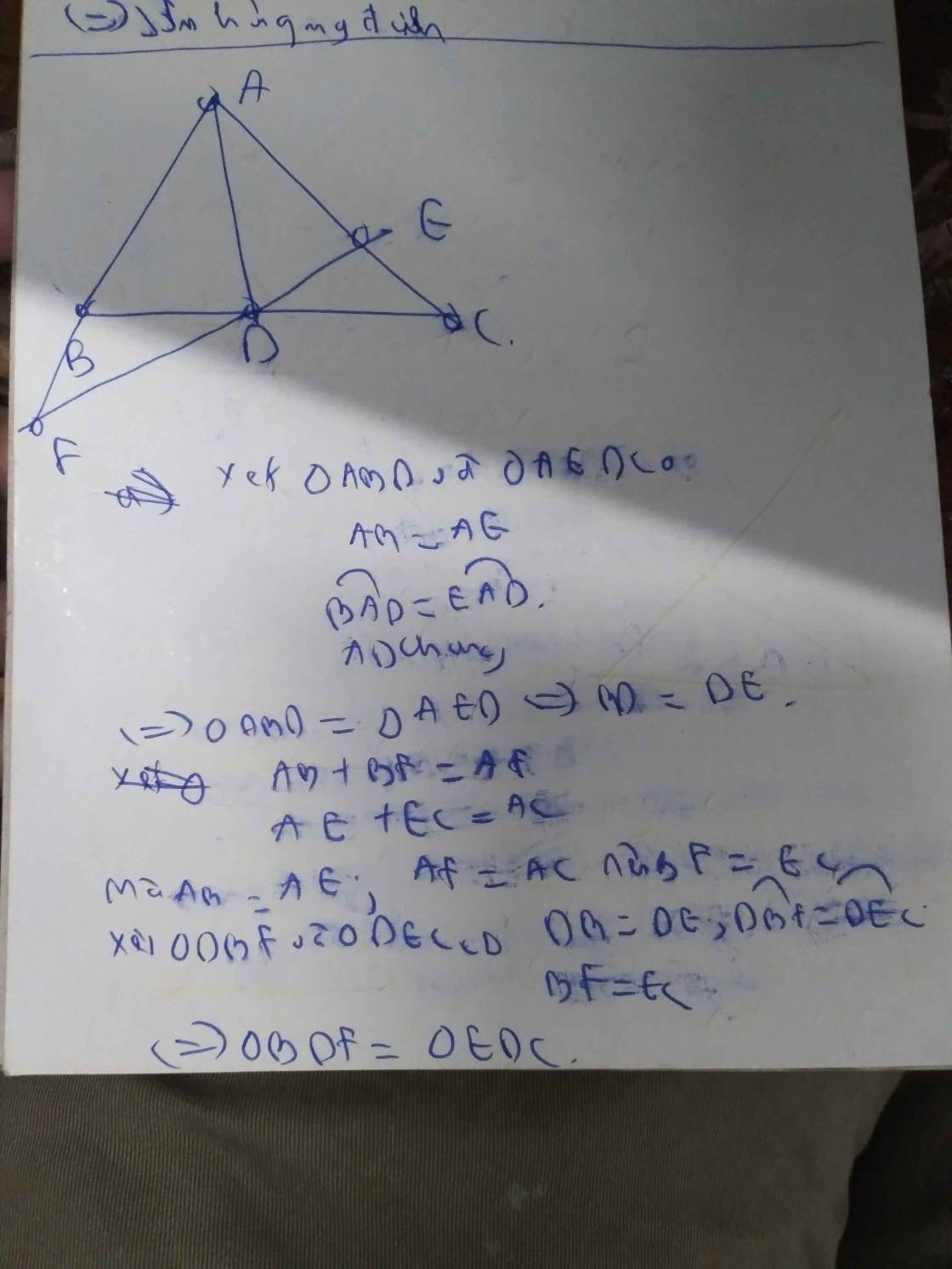
a: Xét ΔABD và ΔAED có
AB=AE
góc BAD=góc EAD
AD chung
=>ΔABD=ΔAED
=>BD=ED
b: AB+BF=AF
AE+EC=AC
mà AB=AE và AF=AC
nên BF=EC
c: Xét ΔDBF và ΔDEC có
DB=DE
góc DBF=góc DEC
BF=EC
=>ΔDBF=ΔDEC
d: AF=AC
DF=DC
=>AD là trung trực của CF
=>AD vuông góc CF

a, Ta có:
ADAB=412=13;AEAC=515=13⇒ADAB=AEAC⇒ADAB=412=13;AEAC=515=13⇒ADAB=AEAC⇒Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.⇒⇒ DE//AE
Xét tam giác ADE và ABC có:
ADAB=AEACADAB=AEAC
ˆDAE=ˆBACDAE^=BAC^
⇒⇒ Tam giác ADF đồng dạng với tam giác ABC
Đọc tiếp

Cho tam giác ABC, AB<AC.Tia p/g của góc A cắt BC ở D, trên tia AC lấy điểm E sao cho AE=AB. Gọi tia M là giao điểm của AB va DE
Cmr: a) tam giác ABD=tam giacd AED
b) tam giacd DBM=tam giác DEC


a) Xét ΔABD và ΔAED có
\(\widehat{A_1}=\widehat{A_2}\)( tia phân giác AD của góc BAC)
AB=AE(GT)
AD chung
Nên ΔABD=ΔAED(c.g.c)
b)Ta có: AF=AC (GT)
=>ΔAFC vuông tại A
Mà AD là đường phân giác=>AD là đường cao
=>AD⊥FC
c)Ta có :ΔABD=ΔAED=>BD=DE(1), \(\widehat{B_1}=\widehat{E_1}\)
Mà \(\widehat{B_1}+\widehat{B_2}=180^o,\widehat{D_1}+\widehat{D_2}=180^o\)
=>\(\widehat{B_2}=\widehat{D_2}\)(2)
tA CÓ:AF=AC, AB=AE=>BF=EC(3)
Từ (1), (2), (3), ta có ΔBDF=ΔEDC(c.g.c)


Ta sẽ nối điểm F với D
Ta có: EF//BC=>EF//BD(D\(\in\)BC)=>^EFD=^BDF(so le trong).
ED//AB=>ED//BF(F\(\in\)AB)=>^BFD=^EDF
Xét tam giác BFD và tam giác EDF:^EFD=^BDF; FD chung; ^BFD=^EDF=> Tam giác BFD = Tam giác EDF (g.c.g)
=>BF=ED(2 cạnh tương ứng). Mà AE=BF=>AE=ED(t/c bắc cầu)
Tam giác BFD=Tam giác EDF=>BD=FE=>^FBD=^FED(2góc tương ứng)
FE//BD=>^FBD=^AFE(đồng vị)
Xét tam giác BFD và tam giác FAE có: ^FBD=^AFE; BD=FE; ^FDB=^AEF=> Tam giác BFD=Tam giác FAE (g.c.g)
=>^BFD=^FAE=>FD//AE. Do FD//AE; ED//AF=>FD=AE; ED=AF(t/c đoạn chắn)
Mà DE=AE(cmt)=>DF=AF=AE=ED=>^FDE=^AED=90o
Xét tam giác FDE và tam giác AED: DE chung; ^FDE=^AED=90o; FD=AE=> Tam giác FDE=Tam giác AED(c.g.c)(1)
FD//EC=>^FDE=^CED(so le trg). FE//DC=>^FED=^CDE(so le trg)
Xét tam giác FED và tam giác CDE: ^FDE=^CED; DE chung; ^FED=^CDE=>Tam giác FED=Tam giác CDE(g.c.g)(2)
Từ (1) và (2)=> Tam giác AED=Tam giác CED=>DA=DC
=>Tam giác BFD=Tam giác DEC(g.c.g)=>DB=DA. mà DA=DC=> Điểm D cách đều AB và AC (đpcm)