Giải bài toán hình Cho đoạn thẳng AD=2a với I là trung điểm , kẻ tia Ix vuông góc với AD, vẽ (O;R) sao cho R>a tiếp xúc với AD tại A, cắt tia Ix tại B,C ( B nằm giữa I và C) . a) Cm IB*IC không đổi khi (O) thay đổi b) Cm B là trực tâm tam giác ADC.Có nhận xét gì về trực tâm tam giác ABC c) Gọi D' đối xứng với D qua AC,chứng minh D' thuộc (O;R)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a,Ta có:AD vuông góc với BC(gt)
BE vuông góc với AD(gt)
Mà AD cắt BE tại H (gt)
Từ đó suy ra H là trực tâm
Mà H thuộc CH,suy ra CH vuông góc AB

Cho đường tròn (O, R). Từ điểm A nằm ngoài (O) kẻ hai tiếp tuyến AB, AC với (O) (B, C là các tiếp điểm)
a, CMR OA là đường trung trực của đoạn BC
b, Gọi D là giao điểm của đoạn thẳng OA với (O). Kẻ dây BE của (O) song song với OD, kẻ bán kính OF vuông góc với CD. Chứng minh C, O, E thẳng hàng và EF là tia phân giác của góc CED
c, Vẽ đường tròn (A, AD). Gọi I, J lần lượt là giao điểm của đường thẳng ED và FD với đường tròn (A) (I, J khác D). Chứng minh rằng góc CEF= góc JID.

a: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Do đó: ΔABD=ΔACE
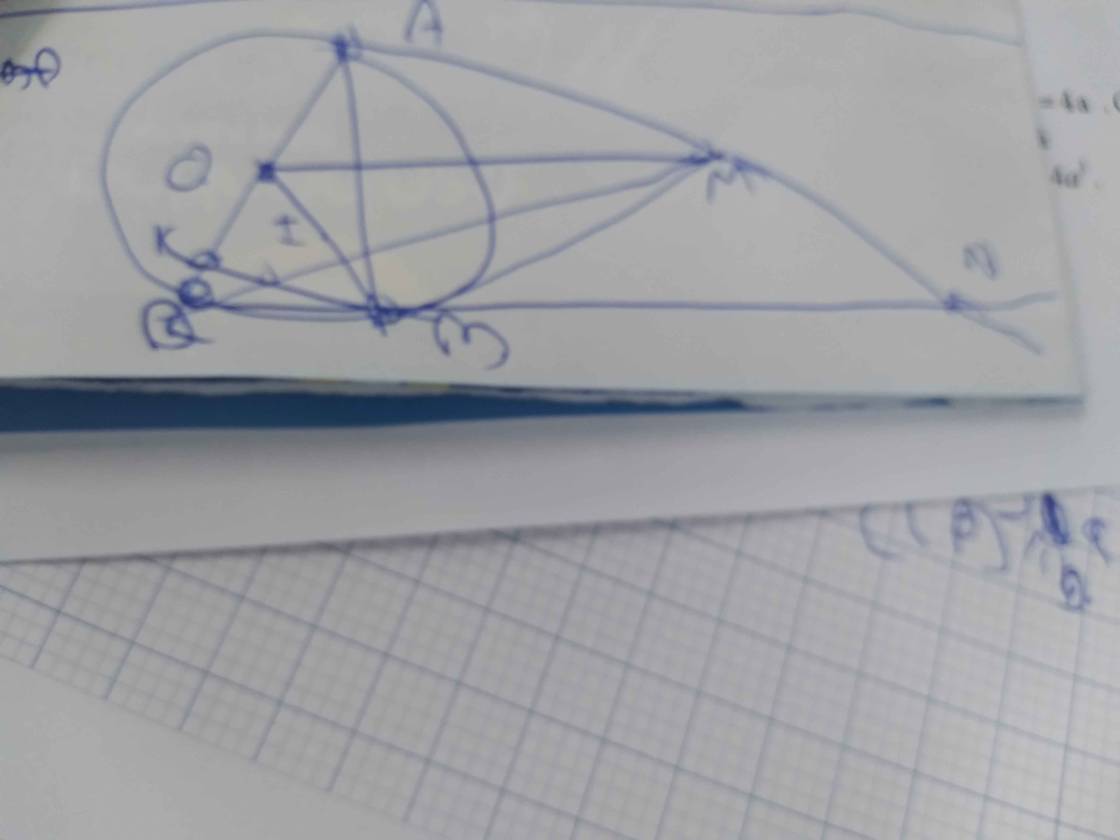

Đường tròn c: Đường tròn qua A với tâm O Đoạn thẳng f: Đoạn thẳng [A, D] Đoạn thẳng i: Đoạn thẳng [I, C] Đoạn thẳng j: Đoạn thẳng [A, O] Đoạn thẳng k: Đoạn thẳng [C, A] Đoạn thẳng l: Đoạn thẳng [C, D] Đoạn thẳng n: Đoạn thẳng [A, E] Đoạn thẳng r: Đoạn thẳng [D, D'] A = (-4.82, 9) A = (-4.82, 9) A = (-4.82, 9) D = (6.09, 9) D = (6.09, 9) D = (6.09, 9) Điểm I: Trung điểm của f Điểm I: Trung điểm của f Điểm I: Trung điểm của f Điểm O: Điểm trên h Điểm O: Điểm trên h Điểm O: Điểm trên h Điểm B: Giao điểm của c, g Điểm B: Giao điểm của c, g Điểm B: Giao điểm của c, g Điểm C: Giao điểm của c, g Điểm C: Giao điểm của c, g Điểm C: Giao điểm của c, g Điểm E: Giao điểm của m, l Điểm E: Giao điểm của m, l Điểm E: Giao điểm của m, l Điểm D': D đối xứng qua k Điểm D': D đối xứng qua k Điểm D': D đối xứng qua k
a. Ta thấy ngay \(\widehat{IAB}=\widehat{ICA}\) (Cùng chắn cung AB)
Vậy thì \(\Delta AIB\sim\Delta CIA\left(g-g\right)\Rightarrow\frac{IA}{IC}=\frac{IB}{IA}\Rightarrow IB.IB=IA^2=a^2\)
Vậy IB.IC không đổi.
b.Ta thấy CI vừa là đường cao, vừa là trung tuyến nên tam giác CAD cân tại C. Vậy \(\widehat{CDA}=\widehat{CAD}\)
Gọi E là giao điểm của AB và CD. Ta có \(\widehat{DAE}=\widehat{ACI}\left(cmt\right)\) nên ta có:
\(\widehat{DAE}+\widehat{EDA}=\widehat{ACI}+\widehat{IAC}=90^o\Rightarrow\widehat{AED}=180^o-90^o=90^o.\)
Vậy AE là đường cao tam giác ADC. Vậy B là trực tâm của tam giác này.
Xét tam giác ABC có: \(CD⊥AB;AD⊥BC;BD⊥AC\), suy ra D là trực tâm của tam giác.
c) Do D' đối xứng với D qua AC nên \(\widehat{D'CA}=\widehat{DCA}\)
Lại có \(\widehat{DCA}=\widehat{DBE}\) (Cùng phụ góc BDC)
Mà \(\widehat{DBE}=\widehat{ABD'}\) (Đối đỉnh) nên \(\widehat{ABD'}=\widehat{D'CA}\)
Xét tứ giác D'CBA có \(\widehat{ABD'}=\widehat{D'CA}\) nên nó là tứ giác nội tiếp. Vậy D thuộc đường tròn qua A, B, C hay thuộc đường tròn (O).