Bài 1: Cho tam giác ABC vuông tại A. Trên cạnh BC lấy điểm E sao cho BE=BA. Qua E kẻ đường thẳng d vuông góc với BC và d cắt AC tại D.a) Tính độ dìa AC khi AB= 9cm, BC= 15cmb) Chứng minh: Tam giác ABD=tam giác EBDc) Gọi H là giao điểm của đường thẳng AB và đường thẳng d. Chứng minh tam giác HBC când) Chứng minh: AD<DCBài 2: Cho tam giác ABC vuông tại A có AB= 12cm, AC= 16cm.Kẻ BF là đường trung tuyến của tam...
Đọc tiếp
Bài 1: Cho tam giác ABC vuông tại A. Trên cạnh BC lấy điểm E sao cho BE=BA. Qua E kẻ đường thẳng d vuông góc với BC và d cắt AC tại D.
a) Tính độ dìa AC khi AB= 9cm, BC= 15cm
b) Chứng minh: Tam giác ABD=tam giác EBD
c) Gọi H là giao điểm của đường thẳng AB và đường thẳng d. Chứng minh tam giác HBC cân
d) Chứng minh: AD<DC
Bài 2: Cho tam giác ABC vuông tại A có AB= 12cm, AC= 16cm.Kẻ BF là đường trung tuyến của tam giác ABC. Từ điểm C kẻ đường thẳng vuông góc với AC cắt đường trung tuyến BF tại D
a) Tính độ dài BC?
b) Chứng minh rằng: Tam giác ABF=tam giác CDF
c) Chứng minh: BF<(AB+BC):2
Bài 3: Cho tam giacsABC vuông tại A; tia phân giác của góc B cắt AC tại D. Kẻ DH vuông góc với BC\(\left(H\in BC\right)\). Gọi K là giao điểm của AB và DH
a) Tính độ dài BC khi AB= 9cm, AC= 12cm
b) Chứng minh: Tam giác ABD=tam giác HBD
c) Chứng minh: Tam giác KDC cân
d) Chứng minh: AB+AC>BD+DC
Bài 4: Cho tam giác ABC vuông tại A. Trên tia BC lấy điểm H sao cho BH=BA. Tia phân giác của góc B cắt AC tại D. Gọi K là giao điểm của AB và DH
a) Tính độ dài BC khi AB= 3cm, AC= 4cm
b) Chứng minh: Tam giác ABD=tam giác HBD
c) Chứng minh \(Dh\perp BC\)
d) So sánh DH với DK


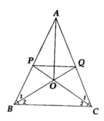
a, BQ là đường phân giác của góc B
=> \(\widehat{B_1}=\widehat{B_2}=\dfrac{1}{2}\widehat{B}\) ( 1 )
CP là đường phân giác của góc C
=> \(\widehat{C_1}=\widehat{C_2}=\dfrac{1}{2}\widehat{C}\) ( 2 )
Mà tam giác ABC cân tại A
= > \(\widehat{B}=\widehat{C}\) ( 3 )
Từ ( 1 ) , ( 2 ) , ( 3 ) = > \(\widehat{B_1}=\widehat{B_2}=\widehat{C_1}=\widehat{C_2}\)
Xét tam giác OBC có :
\(\widehat{B_2}=\widehat{C_2}\) ( cmt )
= > Tam giác OBC cân tại O
b, Do O là giao của 2 đường phân giác BQ và CP của tam giác ABC
nên O là trực tâm của tam giác ABC hay điểm O cách đều 3 cạnh AB,AC, BC của tam giác ABC
c, Do O là trực tâm của tam giác ABC ( câu b, )
Mà tam giác ABC cân tại A
= > AO vừa là đường cao vừa là đường trung tuyến của tam giác ABC tức là AO đi qua trung điểm của đoạn thẳng BC
d, Xét \(\Delta QBC\) và \(\Delta PCB\) có :
\(\widehat{B_2}=\widehat{C_2}\left(cmt\right)\)
BC chung
\(\widehat{B}=\widehat{C}\left(gt\right)\)
=> \(\Delta QBC=\Delta PCB\left(g-c-g\right)\)
= > CP = BQ ( 2 cạnh tương ứng )
e, Do tam giác QBC = tam giác PCB ( câu d, )
=> BP = CQ ( 2 cạnh tương ứng )
\(P\in AB\)
= > AP + PB = AB
= > AP = AB - PB ( 4 )
\(Q\in AC\)
= > AQ + QC =AC
= > AQ = AC - QC ( 5 )
Từ ( 4 ) , ( 5 )
= > AP = AQ
Xét tam giác APQ có :
AP = AQ ( cmt )
= > Tam giác APQ cân tại A ( đpcm )
a) △���△ABC cân tại �A nên ���^=���^ABC=ACB.
Vì ��BQ và ��CP là đường phân giác của �^,�^B,C nên �1^=�2^=���^2B1=B2=2ABC, �1^=�2^=���^2C1=C2=2ACB.
Do đó �1^=�2^=�1^=�2^B1=B2=C1=C2.
Suy ra △���△OBC cân tại �O.
b) Vì �O là giao điểm các đường phân giác ��CP và ��BQ trong △���△ABC nên �O là giao điểm ba đường phân giác trong △���△ABC.
Do đó, �O cách đều ba cạnh ��,��AB,AC và ��BC.
c) Ta có △���△ABC cân tại �,��A,AO là đường phân giác của góc �A nên ��AO đồng thời là trung tuyến và đường cao của △���△ABC.
Vậy đường thẳng ��AO đi qua trung điểm của đoạn thẳng ��BC và vuông góc với nó.
d) Ta có △���=△���△PBC=△QCB (g.c.g)
⇒��=��⇒CP=BQ (hai cạnh tương ứng).
e) Ta có ��=��−��AP=AB−BP, ��=��−��AQ=AC−CQ (1);
△���=△���⇒��=��△PBC=△QCB⇒BP=CQ (2).
Lại có ��=��AB=AC (tam giác ���ABC cân tại �A) (3).
Từ (1), (2) và (3) suy ra ��=��AP=AQ.
Vậy tam giác ���APQ cân tại �A.