Cho $\triangle A B C$ có $A B<A C$. Tia phân giác của $\widehat{A}$ cắt đường thẳng vuông góc với $B C$ tại trung điểm của $B C$ ở $D$. Gọi $H$ và $K$ là chân các đường vuông góc kẻ từ $D$ đến các đường thẳng $A B$, $A C$. Chứng minh $B H=C K$.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 3 2023
a)
Xét \(\Delta AOD\) và \(\Delta COB\) có: \(\left\{{}\begin{matrix}OA=OC\left(gt\right)\\\widehat{O}:chung\\OB=OD\left(gt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta AOD=\Delta COB\left(c.g.c\right)\)
\(\Rightarrow AD=BC\left(\text{2 cạnh tương ứng}\right)\left(\text{đpcm}\right)\)
b)
Nối A với C
Ta có: \(\left\{{}\begin{matrix}OA=OC\\OB=OD\end{matrix}\right.\left(gt\right)\Rightarrow OA-OB=OC-OD\)
Hay \(AB=CD\)
Xét \(\Delta ABC\) và \(\Delta CDA\) có: \(\left\{{}\begin{matrix}AB=CD\left(cmt\right)\\AC:chung\\AD=BC\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta ABC=\Delta DCA\left(c.c.c\right)\)
\(\Rightarrow\widehat{ABC}=\widehat{CDA}\left(\text{2 góc tương ứng}\right)\)
Vì \(\Delta AOD=\Delta COB\left(cmt\right)\Rightarrow\widehat{A}=\widehat{C}\left(\text{2 góc tương ứng}\right)\)
Xét \(\Delta ABE\) và \(\Delta CDE\) có: \(\left\{{}\begin{matrix}\widehat{ABC}=\widehat{CDA}\left(cmt\right)\\AB=CD\left(cmt\right)\\\widehat{A}=\widehat{C}\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta ABE=\Delta CDE\left(g.c.g\right)\left(\text{đpcm}\right)\)
c) Vì \(\Delta ABE=\Delta CDE\left(cmt\right)\Rightarrow AE=CE\left(\text{2 cạnh tương ứng}\right)\)
Xét \(\Delta AOE\) và \(\Delta COE\) có: \(\left\{{}\begin{matrix}OA=OC\left(gt\right)\\\widehat{A}=\widehat{C}\left(cmt\right)\\AE=CE\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta AOE=\Delta COE\left(c.g.c\right)\\ \Rightarrow\widehat{AOE}=\widehat{COE}\left(\text{2 góc tương ứng}\right)\)
`=> OE` là phân giác của \(\widehat{xOy}\) (đpcm)
22 tháng 12 2022
a) Xét ΔABH và ΔACH có:
AH cạnh chung
(AH là tia phân giác của góc BAC)
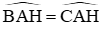
AB = AC (gt)
=> ΔABH = ΔACH (c – g – c)
c.
Gọi I là giao điểm của AH và DE
Xét hai tam giác vuông: ΔADH và ΔAEH có:
AH cạnh chung
(AH là tia phân giác của góc BAC)
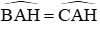
Suy ra: ΔADH = ΔAEH (ch – gn)
Xét ΔADI và ΔAEI có:
AI: cạnh chung
(AH là tia phân giác của góc BAC)
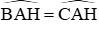
AD = AE (ΔADH = ΔAEH)
=> ΔADI = ΔAEI (c – g – c)
=>\(\left\{{}\begin{matrix}AD=AE\\\widehat{DAI}=\widehat{EAI}\end{matrix}\right.\)
Xét tam giác ADH và tam giác AEH có:
AD = AE
góc DAI = góc EAI
=> tam giác ADH = tam giác AEH (c.g.c)
=> HD = HE (đcpcm)
JW
28 tháng 12 2023
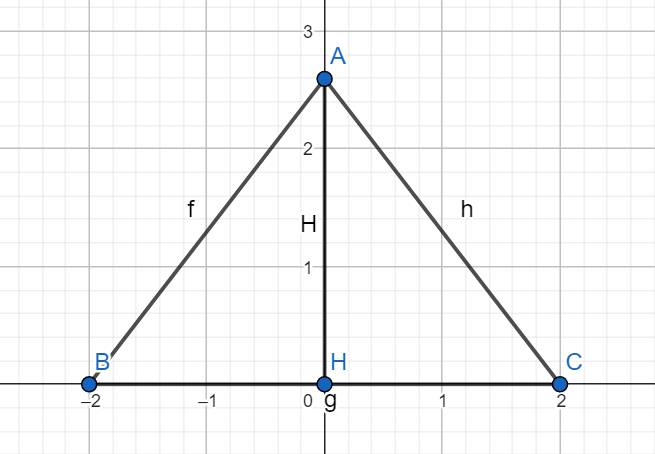
a)
Vì △ABC có AB = AC
\(\rightarrow\)B = C
\(\rightarrow\) △ABC là tam giác cân (2 cạnh đáy bằng nhau)
Xét △ABH và △ ACH có:
AC chung
AB = AC (gt)
BH = CH (H là trung điểm của BC)
\(\Rightarrow\) △ABH = △ACH
b)
Có △ABH = △ACH (câu a)
\(\rightarrow\)góc BAH = góc CAH(2 góc tương ứng)
Mà góc BAH + góc CAH = 180 độ (2 góc kề bù)
\(\rightarrow\) góc BAH = góc CAH = 90 độ
\(\Rightarrow\) AH ⊥ BC
c)
13 tháng 5 2021
- Thể tích của bồn chứa nước đó là 0,735 (m3)
- Diện tích xung quanh là : 15π (cm2)
22 tháng 4 2023
a: Xet ΔABP vuông tại P và ΔACP vuông tại P có
AB=AC
AP chung
=>ΔABP=ΔACP
b: Xét tứ giác ABNC có
P là trung điểm chung của AN và BC
=>ABNC là hình bình hành
=>AB//NC
23 tháng 12 2021
I Find the word which has a different sound in the underlined part.
28 tháng 3 2022
???????????????????????????????????????????????????????????????
D
28 tháng 3 2022
b) Ta có :
\(IB=2IC\Leftrightarrow IB=2\left(IB+BC\right)\Leftrightarrow-IB=2BC\Leftrightarrow BI=2BC\)
\(JC=-\frac{1}{2}JA\Leftrightarrow JB+BC=-\frac{1}{2}\left(JB+BA\right)\)
\(\Leftrightarrow\frac{3}{2}JB=-\frac{1}{2}BA-BC\Leftrightarrow JB=-\frac{1}{3}BA-\frac{2}{3}BC\)
\(\Rightarrow BJ=\frac{1}{3}BA+\frac{2}{3}BC\)
\(\Rightarrow IJ=BJ-BI=\frac{1}{3}BA+\frac{2}{3}BC-2BC=\frac{1}{3}BA-\frac{4}{3}BC\)
\(KA=-KB\Leftrightarrow KB+BA=-KB\Leftrightarrow2KB=-BA\)
\(\Rightarrow2BK=BA\Leftrightarrow BK=\frac{1}{2}BA\)
\(\Rightarrow JK=BK-BJ=\frac{1}{2}BA-\frac{2}{3}BC=\frac{1}{6}BA-\frac{2}{3}BC\)
\(=\frac{1}{2}\left(\frac{1}{3}BA-\frac{4}{3}BC\right)=\frac{1}{2}IJ\)
Vậy \(I,J,K\)thẳng hàng
22 tháng 2 2023
a: BC vuông góc AB
BC vuông góc SA
=>BC vuông góc (SAB)
b: BK vuông góc AC
BK vuôg góc SA
=>BK vuông góc (SAC)
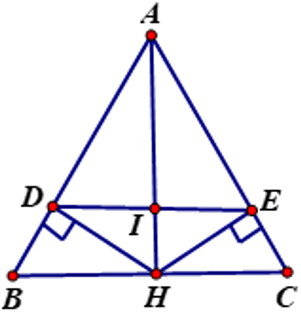
Ta có �D thuộc phân giác của �^A;
��⊥��DH⊥AB; ��⊥��DK⊥AC ⇒��=��⇒DH=DK (tính chất tia phân giác của một góc).
Gọi �G là trung điểm của ��BC.
Xét △���△BGD và △���△CGD, có
���^=���^=90∘BGD=CGD=90∘ (��DG là trung trực của ��BC ),
��=��BG=CG (già thiết),
��DG là cạnh chung.
Do đó △���=△���△BGD=△CGD (hai cạnh góc vuông)
⇒��=��⇒BD=CD (hai cạnh tương ứng).
Xét △���△BHD và △���△CKD, có
���^=���^=90∘BHD=CKD=90∘ (giả thiết);
��=��DH=DK (chứng minh trên);
��=��BD=CD (chứng minh trên).
Do đó △���=△���△BHD=△CKD (cạnh huyền - cạnh góc vuông)
⇒��=��⇒BH=CK (hai cạnh tương ứng).
Ta có DD thuộc phân giác của \widehat{A}A;
D H \perp A BDH⊥AB; D K \perp A CDK⊥AC \Rightarrow D H=D K⇒DH=DK (tính chất tia phân giác của một góc).
Gọi GG là trung điểm của BCBC.
Xét \triangle B G D△BGD và \triangle C G D△CGD, có
\widehat{B G D}=\widehat{C G D}=90^{\circ}BGD=CGD=90∘ (DGDG là trung trực của B CBC ),
BG=CGBG=CG (già thiết),
DGDG là cạnh chung.
Do đó \triangle B G D=\triangle C G D△BGD=△CGD (hai cạnh góc vuông)
\Rightarrow B D=C D⇒BD=CD (hai cạnh tương ứng).
Xét \triangle B H D△BHD và \triangle C K D△CKD, có
\widehat{B H D}=\widehat{C K D}=90^{\circ}BHD=CKD=90∘ (giả thiết);
D H=D KDH=DK (chứng minh trên);
B D=C DBD=CD (chứng minh trên).
Do đó \triangle B H D=\triangle C K D△BHD=△CKD (cạnh huyền - cạnh góc vuông)
\Rightarrow B H=C K⇒BH=CK (hai cạnh tương ứng).