làm hộ em bài 3Nhãn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
làm hộ em bài 1.39
20 tháng 9 2021
1.39:
\(215=2\cdot10^2+1\cdot10^2+5\cdot10^0\)
\(902=9\cdot10^2+0\cdot10^1+2\cdot10^0\)
\(2020=2\cdot10^3+0\cdot10^2+2\cdot10^1+0\cdot10^0\)
13 tháng 7 2021
1)
a) 4y2-4xy+x2= x2-4xy+4y2= (x-2y)2
b) 9x2-12xy+4y2= (3x)2-2.3x.2y+(2y)2= (3x-2y)2
c) 16x2-25=(4x)2-52= (4x-5)(4x+5)
d) 1-9y2= 12-(3y)2=(1-3y)(1+3y)
13 tháng 7 2021
g) x3-27y3= (x-3y)(x2+3xy+9y2)
h) 64 + 8x3=(4+2x)(16+8x+4x2)
13 tháng 1 2022
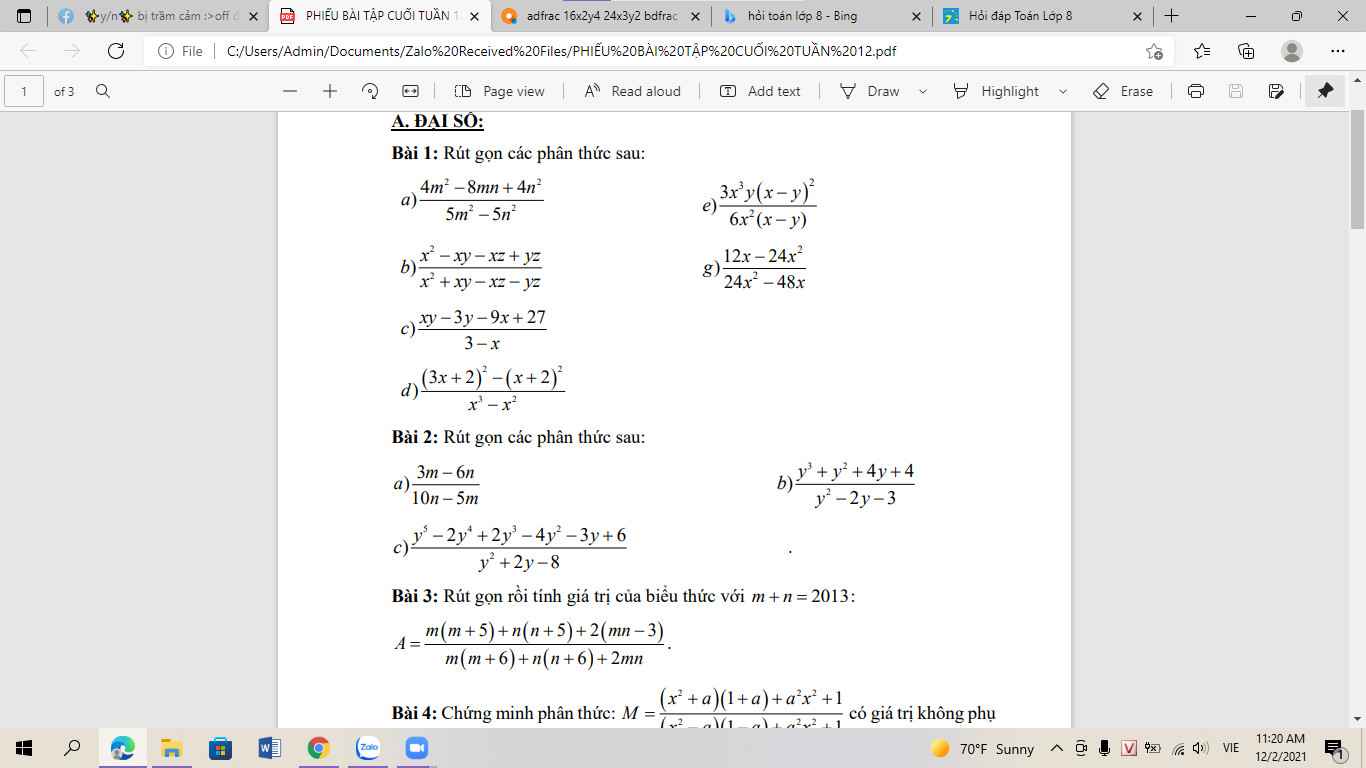
Bài 1:
a: =8xy/2x=4y
b: \(=\dfrac{4x-1-7x+1}{3x^2y}=\dfrac{-3x}{3x^2y}=\dfrac{-1}{xy}\)
c: \(=\dfrac{3x-x+6}{2x\left(x+3\right)}=\dfrac{2\left(x+3\right)}{2x\left(x+3\right)}=\dfrac{1}{x}\)
e: \(=\dfrac{5\left(x+2\right)}{4\left(x-2\right)}\cdot\dfrac{-2\left(x-2\right)}{x+2}=\dfrac{-10}{4}=-\dfrac{5}{2}\)
2 tháng 12 2021
Bài 1:
a) \(=\dfrac{\left(2m-2n\right)^2}{5\left(m^2-n^2\right)}=\dfrac{4\left(m-n\right)^2}{5\left(m-n\right)\left(m+n\right)}=\dfrac{4m-4n}{4m+5n}\)
b) \(=\dfrac{\left(x-y\right)\left(x-z\right)}{\left(x+y\right)\left(x-z\right)}=\dfrac{x-y}{x+y}\)
c) \(=\dfrac{\left(x-3\right)\left(y-9\right)}{-\left(x-3\right)}=9-y\)
d) \(=\dfrac{\left(3x+2-x-2\right)\left(3x+2+x+2\right)}{x^2\left(x-1\right)}=\dfrac{8x\left(x+1\right)}{x^2\left(x-1\right)}=\dfrac{8x+8}{x^2-x}\)
e) \(=\dfrac{xy\left(x-y\right)}{2}=\dfrac{x^2y-xy^2}{2}\)
g) \(=\dfrac{12x\left(1-2x\right)}{24x\left(x-2\right)}=\dfrac{1-2x}{2x-4}\)
Bài 2:
a) \(=\dfrac{3\left(m-2n\right)}{-5\left(m-2n\right)}=-\dfrac{3}{5}\)
b) \(=\dfrac{\left(y+1\right)\left(y^2+4\right)}{\left(y-3\right)\left(y+1\right)}=\dfrac{y^2+4}{y-3}\)
c) \(=\dfrac{y^4\left(y-2\right)+2y^2\left(y-2\right)-3\left(y-2\right)}{\left(y-2\right)\left(y+4\right)}=\dfrac{\left(y-2\right)\left(y^4+2y^2-3\right)}{\left(y-2\right)\left(y+4\right)}=\dfrac{y^4+2y^2-3}{y+4}\)
Bài 3:
\(A=\dfrac{\left(m^2+2mn+n^2\right)+5\left(m+n\right)-6}{\left(m^2+2mn+n^2\right)+6\left(m+n\right)}=\dfrac{\left(m+n\right)^2+5\left(m+n\right)-6}{\left(m+n\right)^2+6\left(m+n\right)}=\dfrac{2013^2+5.2013-6}{2013^2+6.2013}=\dfrac{2012}{2013}\)
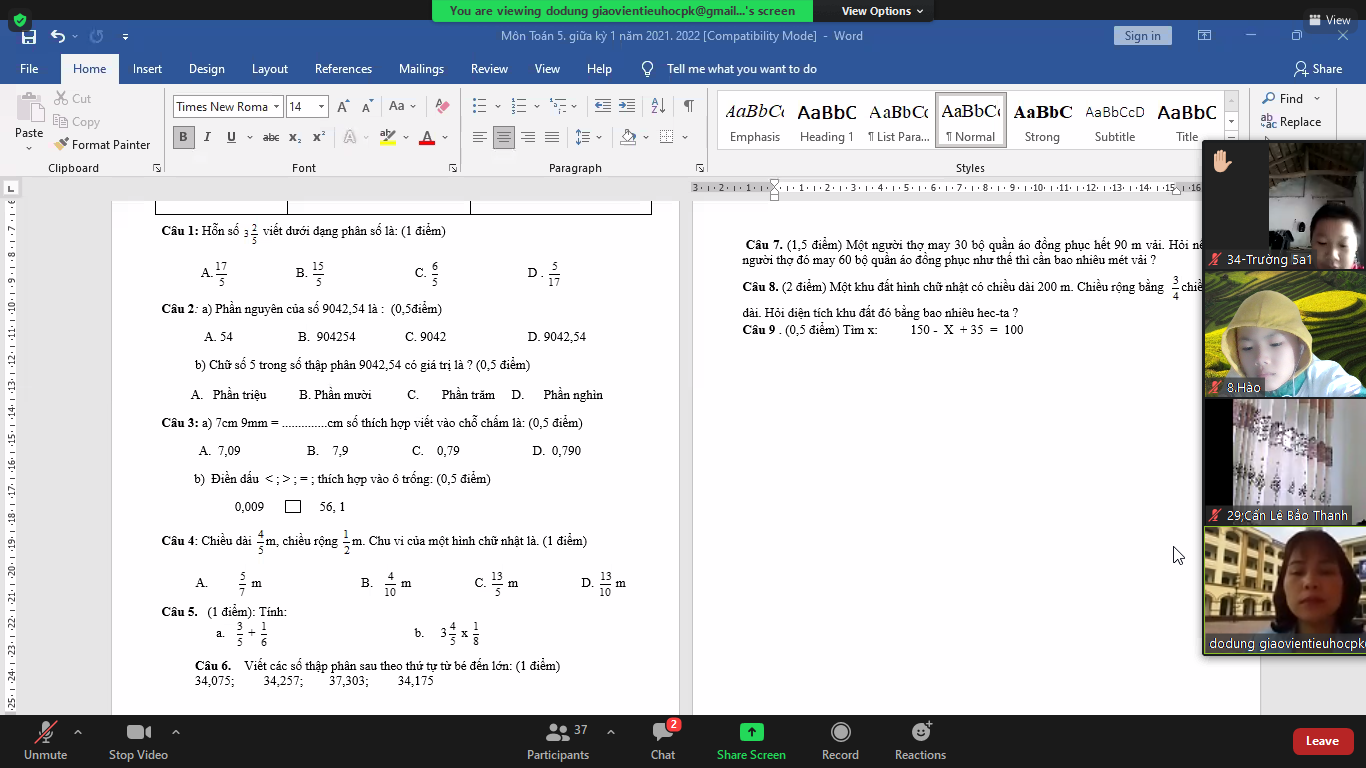
Gọi O là giao điểm AC và BD \(\Rightarrow H\in BO\Rightarrow H\in BD\) do tam giác ABC đều
\(\Rightarrow SH\in\left(SBD\right)\)
Ta có: \(\left\{{}\begin{matrix}AC\perp BD\left(\text{2 đường chéo hình thoi}\right)\\SH\perp\left(ABCD\right)\Rightarrow SH\perp AC\end{matrix}\right.\)
\(\Rightarrow AC\perp\left(SBD\right)\)
b.
\(SH\perp\left(ABCD\right)\Rightarrow SH\) là hình chiếu vuông góc của SB lên (ABCD)
\(\Rightarrow\widehat{SBH}\) là góc giữa SB và (ABCD)
\(BH=\dfrac{2}{3}.\dfrac{a\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{3}\Rightarrow tan\widehat{SBH}=\dfrac{SH}{BH}=\sqrt{6}\) \(\Rightarrow\widehat{SBH}\approx67^048'\)
Theo cm câu a ta có \(AC\perp\left(SBD\right)\) tại O
\(\Rightarrow SO\) là hình chiếu vuông góc của SC lên (SBD)
\(\Rightarrow\widehat{CSO}\) là góc giữa SC và (SBD)
\(OC=\dfrac{1}{2}AC=\dfrac{a}{2}\)
\(OH=\dfrac{1}{3}.\dfrac{a\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{6}\Rightarrow SO=\sqrt{SH^2+OH^2}=\dfrac{5a\sqrt{3}}{6}\)
\(\Rightarrow tan\widehat{CSO}=\dfrac{OC}{SO}=\dfrac{\sqrt{3}}{5}\Rightarrow\widehat{CSO}\approx19^0\)