Phương trình đường thẳng và đồ thị hàm số có khác nhau không ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 12 2020
Pt hoành độ giao điểm:
\(-x^2+2x+3=-2x+1\)
\(\Leftrightarrow x^2-4x-2=0\Rightarrow\left[{}\begin{matrix}x=2+\sqrt{6}\Rightarrow y=-3-2\sqrt{6}\\x=2-\sqrt{6}\Rightarrow y=-3+2\sqrt{6}\end{matrix}\right.\)
Vậy tọa độ giao điểm là: \(\left(2+\sqrt{6};-3-2\sqrt{6}\right)\)
Và \(\left(2-\sqrt{6};-3+2\sqrt{6}\right)\)
T
30 tháng 12 2020
\(\left(P\right):y=-x^2+2x+3\\ \left(d\right):y=-2x+1\)
xét phương trình hoành độ giao điểm của (P) và (d)
\(-x^2+2x+3=-2x+1\)
\(< =>-x^2+4x+2=0\)
\(< =>\left[{}\begin{matrix}x=2+\sqrt{6}\\x=2-\sqrt{6}\end{matrix}\right.\)
thay vào (d) => \(\left[{}\begin{matrix}x=2+\sqrt{6}=>y=-3-2\sqrt{6}\\x=2-\sqrt{6}=>y=-3+2\sqrt{6}\end{matrix}\right.\)
vậy ...
21 tháng 9 2023
a) \(\left(d_1\right):y=-2x-2\)
\(\left(d_2\right):y=ax+b\)
\(\left(d_2\right)//d_1\Leftrightarrow\left\{{}\begin{matrix}a=-2\\b\ne-2\end{matrix}\right.\)
\(\Leftrightarrow\left(d_2\right):y=-2x+b\)
\(M\left(2;-2\right)\in\left(d_2\right)\Leftrightarrow-2.2+b=-2\)
\(\Leftrightarrow b=2\) \(\left(thỏa.đk.b\ne-2\right)\)
Vậy \(\left(d_2\right):y=-2x+2\)
b) \(\left\{{}\begin{matrix}\left(d_1\right):y=-2x-2\\\left(d_2\right):y=-2x+2\end{matrix}\right.\)
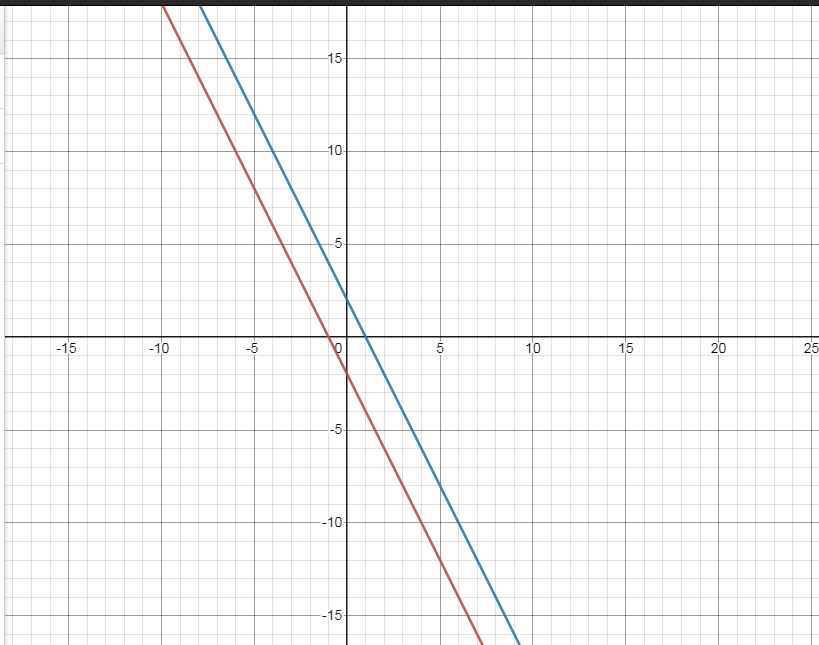
c) \(\left(d_3\right):y=x+m\)
\(\left(d_1\right)\cap\left(d_3\right)=A\left(x;0\right)\Leftrightarrow\left\{{}\begin{matrix}y=x+m\\y=-2x-2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}0=x+m\\0=-2x-2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m=1\\x=-1\end{matrix}\right.\)
\(\Rightarrow\left(d_3\right):y=x+1\)
CM
15 tháng 1 2019
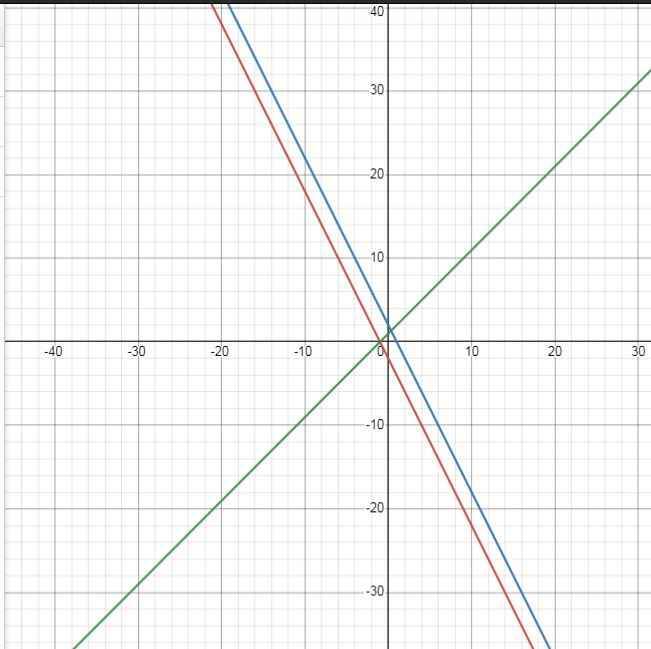
Chọn đáp án B
Do đó x = 2 là tiệm cận đứng của đồ thị hàm số.
13 tháng 9 2015
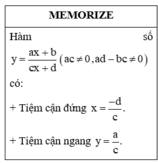
Gọi đường thẳng đi qua A(1;2) có dạng y = ax + b
Vì y = ax+ b // y = 3x + 2008
=> a = 3 ; b khác 2008
=> y = 3x + b
Mà A(1;2) thuộc y = 3x + b
thay x = 1 ; y = 2 ta có :
2 = 3 + b => b = -1
Vậy pt đoạn thẳng đi qua A(1;2) là y =3x - 1
Một mặt, nếu hàm số \(f\left(x\right)\) có đồ thị hàm số không phải là đường thẳng (ví dụ như hàm số \(y=x^2\)) thì sẽ không tồn tại "phương trình đường thẳng của hàm số \(f\left(x\right)\)" nhưng vẫn sẽ tồn tại "đồ thi hàm số \(f\left(x\right)\)".
Mặt khác, cho dù \(f\left(x\right)\) có đồ thị là đường thẳng thì hai khái niệm này vẫn hoàn toàn khác nhau. "Phương trình đường thẳng của \(f\left(x\right)\)" là dùng để chỉ một phương trình đại số, còn "đồ thị hàm số \(f\left(x\right)\)" dùng để chỉ hình vẽ biểu thị hàm số đó.