Cho tam giác ABC M là trung điểm của BC trên tia đối của MA đến điểm B sao cho MA=tam giác MD
a. chứng minh tam giác AMB=tam giác DMC
b. chứng minh AB song song DC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

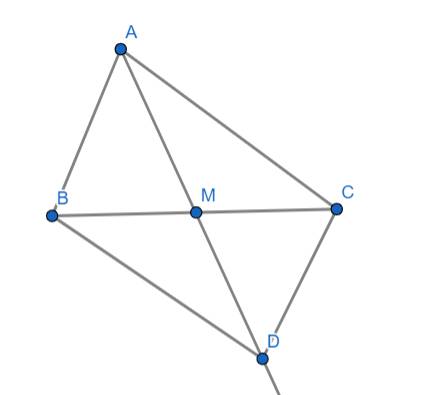
a) Xét ΔAMB và ΔDMC có:
\(AM=CM\) (gt)
\(\widehat{AMB}=\widehat{DMC}\) (đối đỉnh)
\(BM=CM\) (M là trung điểm của BC)
\(\Rightarrow\text{Δ}AMB=\text{Δ}DMC\left(c.g.c\right)\)
b) Ta có: \(\text{Δ}AMB=\text{Δ}DMC\left(cmt\right)\)
\(\Rightarrow AB=DC\) (2 cạnh t.ứng)
c) Ta có: \(\text{Δ}AMB=\text{Δ}DMC\left(cmt\right)\)
\(\Rightarrow\widehat{MAB}=\widehat{MDC}\) (hai góc t.ứng)
Mà hai góc này ở vị trí so le trong
\(\Rightarrow AB//CD\)

a) Xét \(\Delta AMB\)và \(\Delta DMC\)có:
AM = MD (gt)
\(\widehat{AMB}=\widehat{DMC}\)(2 góc đối đỉnh)
MB = MC (M là trung điểm của BC)
\(\Rightarrow\Delta AMB=\Delta DMC\left(c.g.c\right)\)
b) Ta có: \(\Delta AMB=\Delta DMC\)(theo a)
\(\Rightarrow\widehat{BAM}=\widehat{CDM}\)(2 góc tương ứng)
Mà 2 góc này ở vị trí so le trong
\(\Rightarrow AB//CD\)
c) Xét \(\Delta AMB\)và \(\Delta AMC\)có:
AB = AC (gt)
AM là cạnh chung
MB = MC (M là trung điểm của BC)
\(\Rightarrow\Delta AMB=\Delta AMC\left(c.c.c\right)\)
\(\Rightarrow\widehat{AMB}=\widehat{AMC}\)(2 góc tương ứng)
Mà \(\widehat{AMB}+\widehat{AMC}=180^o\)(2 góc kề bù)
\(\Rightarrow\widehat{AMB}=\widehat{AMC}=\frac{180^o}{2}=90^o\)
\(\Rightarrow AM\perp BC\)
d) Mk ko hiểu đề bài cho lắm!!!!!

a) Sửa đề: ΔAMB=ΔDMC
Xét ΔAMB và ΔDMC có
MA=MD(gt)
\(\widehat{AMB}=\widehat{DMC}\)(hai góc đối đỉnh)
MB=MC(M là trung điểm của BC)
Do đó: ΔAMB=ΔDMC(c-g-c)

a: Xét ΔMAB và ΔMDC có
MA=MD
góc AMB=góc DMC
MB=MC
Do đo ΔMAB=ΔMDC
b: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
nên ABDC là hình bình hành
=>AC//BD
c: Xét ΔAHB vuông tại H và ΔDKC vuông tại K có
AB=DC
góc ABH=góc DCK
Do đo: ΔAHB=ΔDKC
=>AH=DK và BK=CH

a: Xét ΔAMB và ΔDMC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔAMB=ΔDMC
b: ΔAMB=ΔDMC
=>\(\widehat{MAB}=\widehat{MDC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//CD
c: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
=>\(\widehat{AMB}=\widehat{AMC}\)
mà \(\widehat{AMB}+\widehat{AMC}=180^0\)(hai góc kề bù)
nên \(\widehat{AMB}=\widehat{AMC}=\dfrac{180^0}{2}=90^0\)
=>AM\(\perp\)BC
XétΔCAD có
CM là đường cao
CM là đường trung tuyến
Do đó: ΔCAD cân tại C
Ta có: ΔCAD cân tại C
mà CM là đường cao
nên CM là phân giác của góc ACD
=>CB là phân giác của góc ACD
câu a :
xét ΔAMB và ΔDMC, ta có :
MB = MC (vì M là trung điểm của BC)
\(\widehat{AMB}=\widehat{DMC}\) (đối đỉnh)
MA = MD (giả thiết)
\(\Rightarrow\Delta AMB=\Delta DMC\left(c.g.c\right)\)
câu b :
\(vì\) \(\Delta AMB=\Delta DMC\) \(nên\) \(\Rightarrow\widehat{ABM}=\widehat{DCM}\) (2 góc tương ứng)
mà 2 góc này ở vị trí so le trong nên => AB // DC
câu a :
xét \(\Delta ADM\) và \(\Delta DMC\), ta có :
\(MB=MC\) (vì M là trung điểm của cạnh BC)
\(\widehat{AMB}=\widehat{DMC}\) (đối đỉnh)
\(MA=MD\) (giả thiết)
\(\Rightarrow\Delta AMB=\Delta DMC\left(c.g.c\right)\)
câu b :
vì \(\Delta AMB=\Delta DMC\) nên \(\Rightarrow\widehat{ABM}=\widehat{DCM}\) (2 góc tương ứng). Mà 2 góc này ở vị trí soletrong nên AB // DC