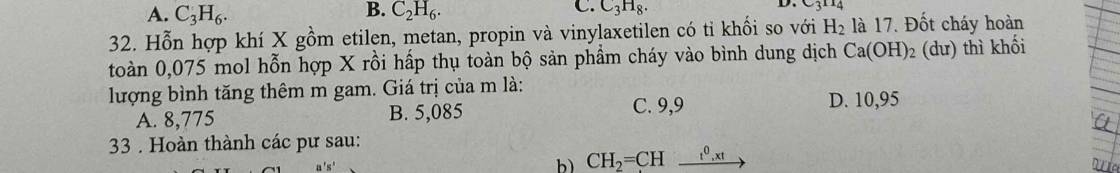Giúp mình câu 32
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
câu 32 , giúp mình với
MH
9 tháng 2 2021
Câu 32:
F1: 599 cao tròn: 213 cao dài: 210 thấp tròn: 65 thấp dài
<=> Tỉ lệ 9A-B- : 3A-bb : 3aaB- : 1aabb
Cây cao dài ở F1: 1/3AAbb : 2/3Aabb, tự thụ phấn:
=> (1/3AAbb : 2/3Aabb) x (1/3AAbb : 2/3Aabb)
Aabb x Aabb => (3/4A-bb:1/4aabb)
AAbb x AAbb => 1AAbb
=> Xác suất cần tìm là: 2/3*3/4 + 1/3 = 5/6
23 tháng 2 2023
Câu 31:
PT: \(CH_2=CH_2+H_2O\underrightarrow{t^o,xt}CH_3CH_2OH\)
→ Đáp án: A
Câu 32:
Ta có: \(n_{CO_2}=\dfrac{5,6}{22,4}=0,25\left(mol\right)\)
\(n_X=\dfrac{1,12}{22,4}=0,05\left(mol\right)\)
Gọi CTPT của X là CnH2n.
\(\Rightarrow n=\dfrac{n_{CO_2}}{n_X}=5\)
Vậy: X là C5H10.
→ Đáp án: D
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 3 2021
\(=\lim\limits_{x\rightarrow0}\dfrac{\sqrt{4x+1}-\left(2x+1\right)+2x+1-\sqrt[3]{6x+1}}{x^2}\)
\(=\lim\limits_{x\rightarrow0}\dfrac{-\dfrac{4x^2}{\sqrt{4x+1}+2x+1}+\dfrac{x^2\left(8x+12\right)}{\left(2x+1\right)^2+\left(2x+1\right)\sqrt[3]{6x+1}+\sqrt[3]{\left(6x+1\right)^2}}}{x^2}\)
\(=\lim\limits_{x\rightarrow0}\left(-\dfrac{4}{\sqrt{4x+1}+2x+1}+\dfrac{8x+12}{\left(2x+1\right)^2+\left(2x+1\right)\sqrt[3]{6x+1}+\sqrt[3]{\left(6x+1\right)^2}}\right)\)
\(=\dfrac{-4}{1+1}+\dfrac{12}{1+1+1}=2\)
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 3 2022
ĐKXĐ: \(x< 2\)
\(m\sqrt{2-x}=\dfrac{x^2-2mx+2}{\sqrt{2-x}}\Rightarrow m\left(2-x\right)=x^2-2mx+2\)
\(\Leftrightarrow x^2+2=m\left(x+2\right)\Rightarrow m=\dfrac{x^2+2}{x+2}\)
Xét hàm \(f\left(x\right)=\dfrac{x^2+2}{x+2}\) với \(0< x< 2\)
\(f'\left(x\right)=\dfrac{2x\left(x+2\right)-\left(x^2+2\right)}{\left(x+2\right)^2}=\dfrac{x^2+4x-2}{\left(x+2\right)^2}=0\Rightarrow x=-2+\sqrt{6}\)
\(f\left(0\right)=1;f\left(2\right)=\dfrac{3}{2};f\left(-2+\sqrt{6}\right)=-4+2\sqrt{6}\)
\(\Rightarrow-4+2\sqrt{6}\le m< \dfrac{3}{2}\)
\(\Rightarrow m=1\)
Có đúng 1 giá trị nguyên m thỏa mãn
27 tháng 3 2023
Câu 21:
\(n_{C_6H_6}=\dfrac{6,24}{78}=0,08\left(mol\right)\)
\(n_{HNO_3}=\dfrac{13,23}{63}=0,21\left(mol\right)\)
PT: \(C_6H_6+3HNO_3\underrightarrow{^{t^o,xt}}C_6H_3\left(NO_2\right)_3+3H_2O\)
Xét tỉ lệ: \(\dfrac{0,08}{1}>\dfrac{0,21}{3}\), ta được C6H6 dư.
Theo PT: \(n_{C_6H_3\left(NO_2\right)_3\left(LT\right)}=\dfrac{1}{3}n_{HNO_3}=0,07\left(mol\right)\)
\(\Rightarrow m_{C_6H_3\left(NO_2\right)_3\left(LT\right)}=0,07.213=14,91\left(g\right)\)
\(\Rightarrow H\%=\dfrac{10,1388}{14,91}.100\%=68\%\)
→ Đáp án: A
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 3 2021
Ở đây chỉ thấy các câu 26, 32, 34, 36
26.
\(S_{ABC}=\dfrac{1}{2}AB^2=\dfrac{a^2}{18}\)
\(BC=AB\sqrt{2}=\dfrac{a\sqrt{2}}{3}\Rightarrow p=\dfrac{AB+AC+BC}{2}=\dfrac{2a+a\sqrt{2}}{6}\)
\(\Rightarrow r=\dfrac{S}{p}=\dfrac{6a^2}{18a\left(2+\sqrt{2}\right)}=\dfrac{\left(2-\sqrt{2}\right)a}{6}\)
32.
Đường thẳng nhận \(\overrightarrow{n}=\left(5;-1\right)\) là 1 vtpt
34.
Áp dụng định lý hàm cos:
\(c=\sqrt{a^2+b^2-2ab.cosC}=\sqrt{8^2+7^2-2.8.7.cos60^0}=\sqrt{57}\)
36.
\(y=\sqrt{\dfrac{x^2-2mx+5m}{2021}}\)
Hàm xác định trên R khi và chỉ khi: \(x^2-2mx+5m\ge0\) ; \(\forall x\)
\(\Leftrightarrow\Delta'=m^2-5m\le0\Rightarrow0\le m\le5\)
Có 5 giá trị nguyên dương của m thỏa mãn (1;2;3;4;5)
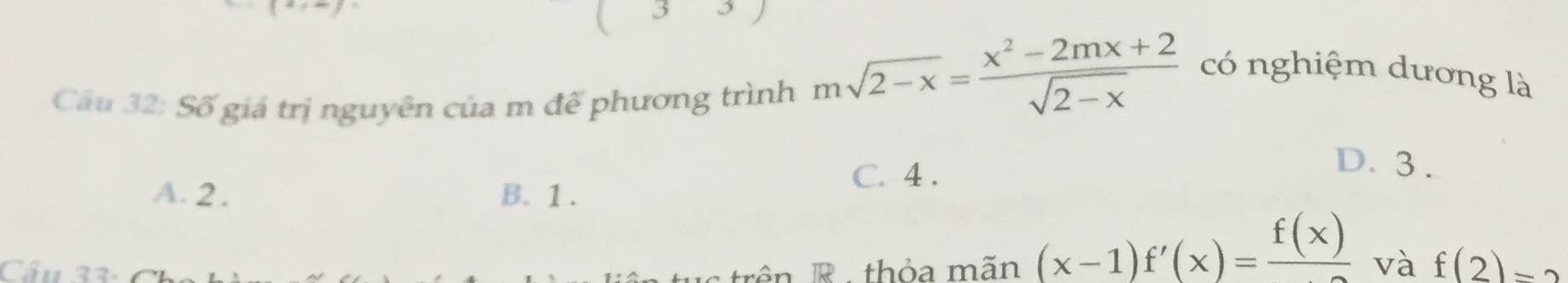
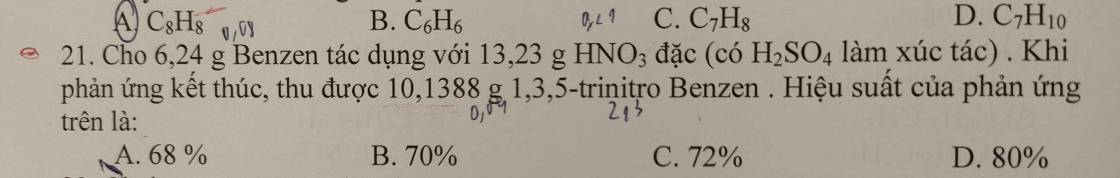
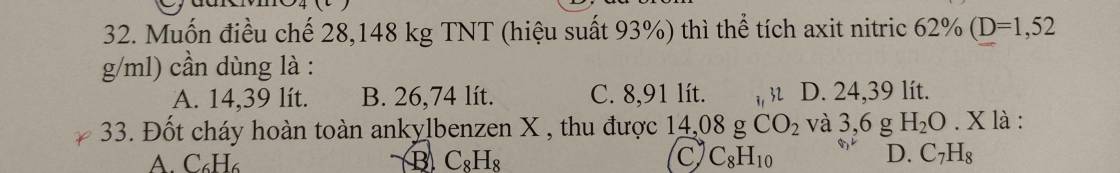
\(M_X=17.2=34\left(g/mol\right)\)
Quy đổi hh \(X\left\{{}\begin{matrix}CH_4\\C_2H_4\\C_3H_4\\C_4H_4\end{matrix}\right.\rightarrow C_xH_4\left(1< x< 4\right)\)
\(m_X=34.0,075=2,55\left(g\right)\)
Mà \(n_H=4n_X=0,3\left(mol\right)\Rightarrow n_C=\dfrac{2,55-0,3}{12}=0,1875\left(mol\right)\)
BTNT: \(\left\{{}\begin{matrix}n_{CO_2}=n_C=0,1875\left(mol\right)\\n_{H_2O}=\dfrac{1}{2}n_H=0,15\left(mol\right)\end{matrix}\right.\)
\(\Rightarrow m=m_{CO_2}+m_{H_2O}=0,1875.44+0,15.18=10,95\left(g\right)\)
Chọn D