Cho đa thức:f(x)=\(ax^2\)+bx+c với a,b,c là các số thực.Biết f(0),f(1),f(2) có giá trị nguyên.Chứng minh 2a,2b có giá trị nguyên
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
H
hnamyuh
27 tháng 2 2023
Đúng(3)
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
2 tháng 3 2021
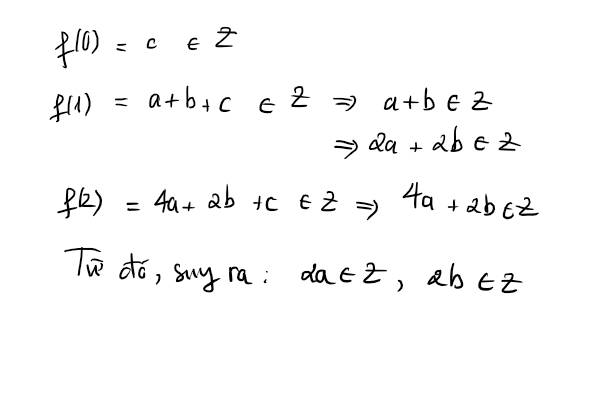
Lời giải:
$f(0)=a.0^2+b.0+c=c$ nguyên
$f(1)=a+b+c$ nguyên, mà $c$ nguyên nên $a+b+c-c=a+b$ nguyên
$f(2)=4a+2b+c=2a+2(a+b)+c$ nguyên mà $a+b, c$ nguyên nên $2a$ nguyên
$2a$ nguyên, $2(a+b)$ nguyên nên $2b$ nguyên.
Ta có đpcm.
22 tháng 2 2019
Ta có:
\(f\left(0\right)=c\in Z\)(1)
\(f\left(1\right)=a+b+c\in Z\)(2)
\(f\left(2\right)=4a+2b+c\in Z\)(3)_
Từ (1), (2) => \(a+b\in Z\)=> \(2a+2b\in Z\)(4)
Từ (1), (3)=> 4a+2b\(\in Z\)(5)
Từ (4), (5) => \(\left(4a+2b\right)-\left(2a+2b\right)\in Z\)
=> \(2a\in Z\)=> \(2b\in Z\)
30 tháng 5 2020
\(f\left(0\right)=a.0^2+b.0+c=c\) có giá trị nguyên
\(f\left(1\right)=a+b+c\) có giá trị nguyên => a + b có giá trị nguyên
\(f\left(2\right)=4a+2b+c=2a+2\left(a+b\right)+c\)=> 2a có giá trị nguyên
=> 4a có giá trị nguyên
=> 2b có giá trị nguyên.
19 tháng 3 2018
) f(0) = c; f(0) nguyên => c nguyên (*)
f(1) = a+ b + c ; f(1) nguyên => a+ b + c nguyên (**)
f(2) = 4a + 2b + c ; f(2) nguyên => 4a + 2b + c nguyên (***)
Từ (*)(**)(***) => a + b và 4a + 2b nguyên
4a + 2b = 2a + 2.(a + b) có giá trị nguyên mà 2(a+ b) nguyên do a+ b nguyên
nên 2a nguyên => 4a có giá trị nguyên mà 4a + 2b nguyên do đó 2b có giá trị nguyên
:3
WH
25 tháng 3 2018
Có \(f\left(0\right);f\left(1\right);f\left(2\right)\)\(\in Z\Rightarrow\hept{\begin{cases}f\left(0\right)=c\in Z\\f\left(1\right)=a+b+c\in z\\f\left(2\right)=4a+2b+c\in z\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}a+b\in z\\4a+2b\in z\end{cases}\Rightarrow\hept{\begin{cases}2a+2b\in z\\4a+2b\in z\end{cases}}\Rightarrow2a\in z;}2b\in z\)
\(\RightarrowĐPCM\)
10 tháng 11 2016
Giả sử f(0), f(1), f(2) có giá trị nguyên là m,n,p. Theo đề bài ta có
\(1\hept{\begin{cases}c=m\left(1\right)\\a+b+c=n\left(2\right)\\4a+2b+c=p\left(3\right)\end{cases}}\)
Ta lấy (3) - 2(2) + (1) vế theo vế ta được
2a = p - 2n + m
=> 2a là số nguyên
Ta lấy 4(2) - (3) - 3(1) vế theo vế ta được
2b = 4n - p - 3m
=> 2b cũng là số nguyên
12 tháng 4 2017
*f(0) nguyên suy ra 0+0+c=c nguyên
*Vì c nguyên và f(1)=a+b+c nguyên suy ra a+b nguyên
*Tương tự vs f(2)=4a+2b+c suy ra 2a nguyên (Vì 4a+2b và 2(a+b) đều nguyên)
Vì 2a và 2(a+b) nguyên suy ra 2b nguyên (đpcm)
15 tháng 8 2015
a) f(0) = c; f(0) nguyên => c nguyên (*)
f(1) = a+ b + c ; f(1) nguyên => a+ b + c nguyên (**)
f(2) = 4a + 2b + c ; f(2) nguyên => 4a + 2b + c nguyên (***)
Từ (*)(**)(***) => a + b và 4a + 2b nguyên
4a + 2b = 2a + 2.(a + b) có giá trị nguyên mà 2(a+ b) nguyên do a+ b nguyên
nên 2a nguyên => 4a có giá trị nguyên mà 4a + 2b nguyên do đó 2b có giá trị nguyên
b) f(3) = 9a + 3b + c = (a+ b + c) + (4a + 2b) + 4a
Vì a+ b + c ; 4a + 2b; 4a đều có giá trị nguyên nên f(3) có giá trị nguyên
f(4) = 16a + 4b + c = (a+ b) + (9a + 3b + c) + 3. 2a
Vì a+ b; 9a + 3b + c; 2a đều nguyên nên f(4) có giá trị nguyên
f(5) = 25a + 5b + c = (16a + 4b + c) + (a+ b) + 4. 2a
Vì 16a + 4b + c ; a+ b; 2a đều có giá trị nguyên nên f(5) có giá trị nguyên
ML
8 tháng 8 2015
\(+f\left(0\right)=c\in Z\Rightarrow c\in Z\)
\(+f\left(2n\right)=4n^2.a+2n.b+c\in Z\Rightarrow n\left(4n.a+2b\right)\in Z\Rightarrow4n.a+2b\in Z\)với mọi số nguyên n.
\(+f\left(2n+1\right)=\left(4n^2+4n+1\right).a+\left(2n+1\right).b+c=\left(4n^2.a+2n.b\right)+\left(4n+1\right)a+b+c\in Z\) \(\Rightarrow\left(4n+1\right)a+b\in Z\)với mọi số nguyên n.
Suy ra: \(\left(8n+2\right)a+2b-\left(4n.a+2b\right)=\left(4n+2\right)a=\left(2n+1\right).2a\in Z\)với mọi số nguyên n
\(\Rightarrow2a\in Z\)
Mà \(4n.a+2b=2.2a+2b\in Z\)
\(\Rightarrow2b\in Z\)
Vậy \(2a,\text{ }2b,\text{ }c\in Z\)