Giải hộ bài 2 với
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 2:
a: Vì (d) có hệ số góc là 3 nên a=3
Vậy: (d): y=3x+b
Thay x=1 và y=0 vào (d), ta được:
b+3=0
hay b=-3
b: Vì (d)//y=0,5x-2 nên a=0,5
Vậy: (d): y=0,5x+b
Thay x=0 và y=2 vào (d), ta được:
b=2


Bài 2:
Thay x=2, y=3 vào M ta có:
\(M=5xy-10+2y=5.3.2-10+3.3=30-10+9=29\)
Bài 3:
\(a,A=\left(2x^3y\right)\left(-3xy\right)=-6x^4y^2\)
Hệ số: -6
Bậc:6
\(b,B=\left(-\dfrac{1}{16}x^2y^2\right)\left(4x^3\right)\left(8xyz\right)=-2x^6y^3z\)
Hệ số: -2
Bậc:10
\(c,\dfrac{-3}{25}x\left(\dfrac{1}{3}x^3y\right)^2\left(\dfrac{5}{2}y^3\right)^2=\dfrac{-3}{25}x\left(\dfrac{1}{9}x^6y^2\right)\left(\dfrac{25}{4}y^6\right)=-\dfrac{1}{12}x^7y^8\)
Hệ số: -1/12
Bậc:15

Câu 3:
a: Xét (O) có
ΔAHC nội tiếp
AC là đường kính
Do đó: ΔAHC vuông tại H
hay AH\(\perp\)BC
b: Ta có: ΔAHB cân tại H
mà HM là đường trung tuyến
nên HM=AM=BM=AB/2
Xét ΔOAM và ΔOHM có
OA=OH
OM chung
AM=HM
Do đó: ΔOAM=ΔOHM
Suy ra: \(\widehat{OAM}=\widehat{OHM}=90^0\)
hay MH là tiếp tuyến của (O)
c: Xét ΔDCE và ΔDAC có
\(\widehat{CDA}\) chung
\(\widehat{DCE}=\widehat{DAC}\)
Do đó: ΔDCE\(\sim\)ΔDAC
Suy ra: DC/DA=DE/DC
hay \(DC^2=DA\cdot DE\)


Bài 5:
CTPT: CxHyO
\(n_{CaCO_3}=\dfrac{40}{100}=0,4\left(mol\right)\)
PTHH: 2CxHyO + \(\dfrac{4x+y-2}{2}\)O2 --to--> 2xCO2 + yH2O
\(\dfrac{0,4}{x}\)<--\(\dfrac{0,4\left(4x+y-2\right)}{4x}\)<------0,4
Ca(OH)2 + CO2 --> CaCO3 + H2O
0,4<-----0,4
=> \(M_{C_xH_yO}=\dfrac{7,4}{\dfrac{0,4}{x}}=18,5x\left(g/mol\right)\)
=> y + 16 = 6,5x (1)
Có \(n_{O_2}=\dfrac{19,2}{32}=0,6\left(mol\right)\)
=> \(\dfrac{0,4\left(4x+y-2\right)}{4x}=0,6\)
=> 0,8x = 0,4y - 0,8 (2)
(1)(2) => x = 4; y = 10
CTPT: C4H10O

Bài 4.
a.OB+ AB = OA
=> AB = OA - OB = 6-3 = 3 cm
b.Ta có: AB = OB = 3cm
=> A là trung điểm của OB
c.Ta có: AC + BC = AB
=> 1,5 + BC = 3
=> BC = 3-1,5 = 1,5 cm

b) \(\dfrac{3\pi}{2}< \alpha< 2\pi\)\(\Rightarrow cos\alpha>0;sin\alpha< 0\)
Có \(1+tan^2\alpha=\dfrac{1}{cos^2\alpha}\)\(\Rightarrow cos\alpha=\dfrac{4}{5}\)
\(sin\alpha=-\sqrt{1-cos^2\alpha}=-\dfrac{3}{5}\)
\(sin\left(\alpha-\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}\left(sin\alpha-cos\alpha\right)=\dfrac{\sqrt{2}}{2}\left(-\dfrac{3}{5}-\dfrac{4}{5}\right)=-\dfrac{7\sqrt{2}}{10}\)
Bài 2:
a) Gọi đt d vuông góc với đường thẳng \(\Delta\)có dạng: \(d:-4x+3y+c=0\)
\(A\in\left(d\right)\Rightarrow-4+3+c=0\Leftrightarrow c=1\)
Vậy \(d:-4x+3y+1=0\)
b) Gọi pt đường tròn (C) tâm A có dạng \(\left(C\right):\left(x-1\right)^2+\left(y-1\right)^2=R^2\)
Vì (C) tiếp xúc với \(\Delta\)
\(\Rightarrow\)\(R=d_{\left(A;\Delta\right)}=\dfrac{\left|3+4+5\right|}{\sqrt{3^2+4^2}}=\dfrac{12}{5}\)
\(\Rightarrow\left(C\right):\left(x-1\right)^2+\left(y-1\right)^2=\dfrac{144}{25}\)
Vậy...


 giải hộ mình bài 2 với ạ
giải hộ mình bài 2 với ạ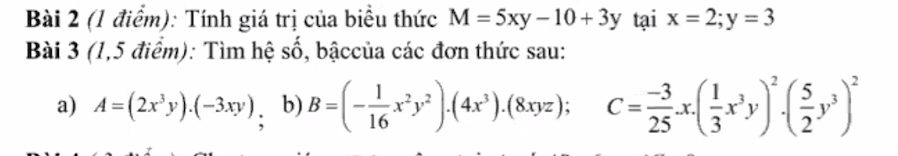
 giải hộ mình 2 bài cuối với
giải hộ mình 2 bài cuối với


