cho (O) và điểm M nằm ngoài đường tròn qua M kẻ tiếp tuyến MI và cát tuyến MCD với (O). CM MI^2 = MC.MD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 2 2023
Xét ΔMBC và ΔMDB có
góc MBC=góc MDB
góc BMC chung
=>ΔMBC đồng dạng với ΔMDB
=>MB/MD=MC/MB
=>MB^2=MD*MC
19 tháng 3 2022
a, Xét tam giác MAD và tam giác MCA có
^M _ chung
^MDA = ^MAC ( cùng chắn cung CA )
Vậy tam giác MAD ~ tam giác MCA (g.g)
\(\dfrac{MA}{MC}=\dfrac{MD}{MA}\Rightarrow MA^2=MD.MC\)(1)
b, Vì MA là tiếp tuyến đường tròn (O) với A tiếp điểm
Lại có OA = OB = R ; MA = MB ( tc tiếp tuyến cắt nhau )
=> OM là trung trực đoạn BA
Xét tam giác MAO đường cao AH ta có
\(MA^2=MO.MH\)(2)
Từ (1) ; (2) suy ra \(MO.MH=MD.MC\)
31 tháng 1 2023
Xét ΔMBC và ΔMDA có
góc MBC=góc MDA
góc DMA chung
=>ΔMBC đồng dạng với ΔMDA
=>MB/MD=MC/MA
=>MB*MA=MD*MC
VV
22 tháng 4 2023
vì AM là tiếp tuyến của ( O) => OA⊥AM =>ΔOAM vuông ở A
=> điểm A thuộc đường tròn đường kính OM
vì BM là tiếp tuyến của (O) => OB⊥BM =>ΔOBM vuông ở B
=> điểm B thuộc đường tròn đường kính OM
Vì OH⊥MI=>ΔOHM vuông tại H
=> điểm H thuộc đường tròn đường kính OM
=> 4 điểm O,A,M,B,H cùng thuộc đường tròn đường kính OM
5 tháng 10 2019
1234 m ngu k bt trả lời thì thôi đừng ở đó xàm xàm trên trang của t này câm k đừng trách t nhắn với pm với admin xóa cái acc của m!
1
1 tháng 10 2019
Mất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcvMất nick đau lòng con quốc quốc
27 tháng 2 2021
a) Xét tứ giác MAOB có
\(\widehat{OAM}\) và \(\widehat{OBM}\) là hai góc đối
\(\widehat{OAM}+\widehat{OBM}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: MAOB là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
b) Xét (O) có
\(\widehat{ADC}\) là góc nội tiếp chắn \(\stackrel\frown{AC}\)
\(\widehat{CAM}\) là góc tạo bởi dây cung CA và tiếp tuyến AM
Do đó: \(\widehat{ADC}=\widehat{CAM}\)(Hệ quả góc tạo bởi tia tiếp tuyến và dây cung)
hay \(\widehat{MDA}=\widehat{MAC}\)
Xét ΔMDA và ΔMAC có
\(\widehat{MDA}=\widehat{MAC}\)(cmt)
\(\widehat{AMD}\) là góc chung
Do đó: ΔMDA∼ΔMAC(g-g)
⇔\(\dfrac{MD}{MA}=\dfrac{MA}{MC}\)(Các cặp cạnh tương ứng tỉ lệ)
⇔\(MA^2=MC\cdot MD\)(đpcm)(1)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔOAM vuông tại A có AH là đường cao ứng với cạnh huyền OM, ta được:
\(MA^2=MH\cdot MO\)(2)
Từ (1) và (2) suy ra \(MH\cdot MO=MC\cdot MD\)(đpcm)
PO
10 tháng 4 2022
c) để chứng minh EC là tiếp tuyến:
chứng minh tứ giác OECH nội tiếp thì ta sẽ có góc OHE=OCE=90o(đpcm)
=> cần chứng minh tứ giác OECH nội tiếp:
ta có: DOC=DHC (ccc CD)
xét MHC=MDO (tam giác MCH~MOD)= OCD (vì DO=OC)=OHD (cùng chắn OD) => HA là phân giác CHD
DOC=DHC => 1/2 DOC= 1/2 DHC =COE=CHE
mà COE với CHE cùng chắn cung CE trong tứ giác OHCE nên tứ giác đấy nội tiếp => xong :))))
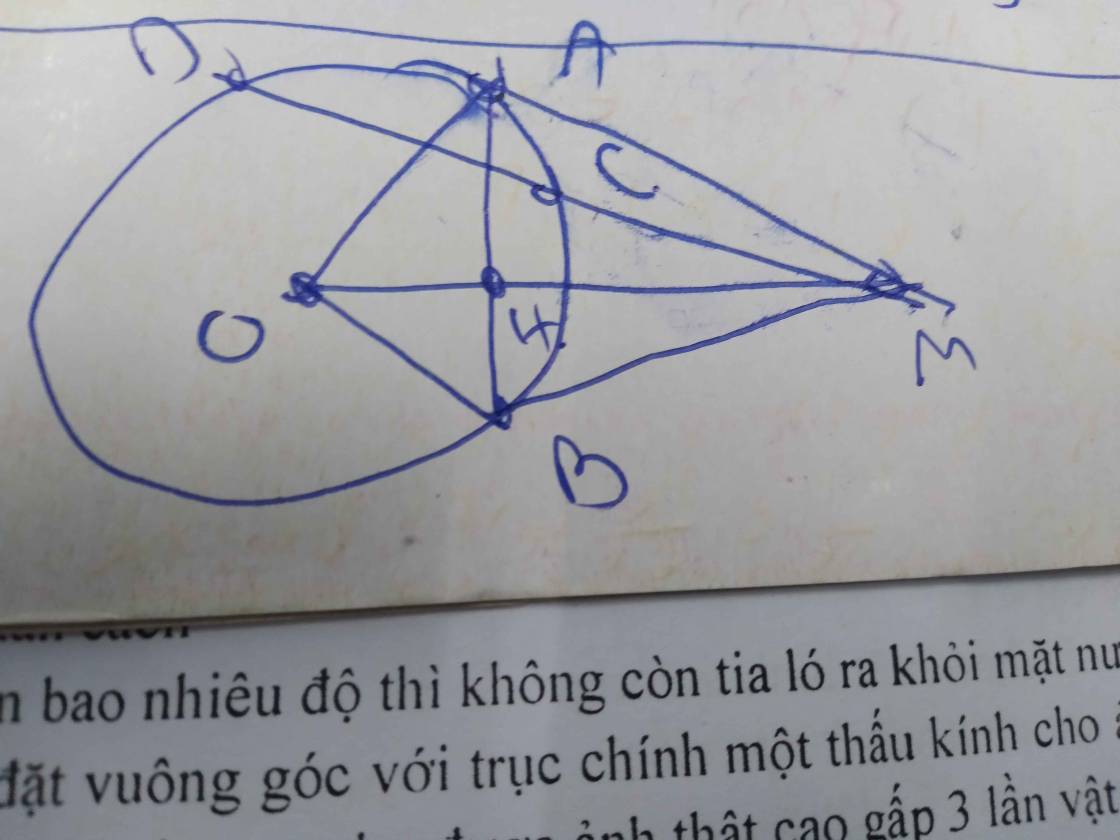
Xét hai tam giác IMC và DMI có:
\(\left\{{}\begin{matrix}\widehat{IDM}\text{ chung}\\\widehat{CIM}=\widehat{IDM}\left(\text{góc nội tiếp và góc tiếp tuyến cùng chắn cung IM}\right)\end{matrix}\right.\)
\(\Rightarrow\Delta IMC\sim\Delta DMI\) (g.g)
\(\Rightarrow\dfrac{MI}{DM}=\dfrac{MC}{MI}\Rightarrow MI^2=MC.MD\) (đpcm)