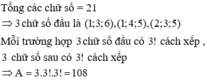Có thể lập được bảo nhiêu số tự nhiên nhỏ hơn 300 từ các chữ số 2,6,1 hoặc 3, biết rằng mỗi chữ số chỉ được dùng một lần trong 1 số bất kì
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
31 tháng 7 2023
Số chia hết cho 9 mà mỗi số xuất hiện 1 lần.
Ta có: 1+2+3+4+5+6=21
Vậy các số chia hết cho 9 sẽ có tổng các chữ số là 9 hoặc 18
Số có 2 chữ số: 36; 63; 45; 54 => 4 số
Số có 3 chữ số: 126; 621; 162; 612; 216; 261; 234; 243; 342; 324; 432; 423; 135; 153; 351; 315; 513; 531 => 18 số
Số có 4 chữ số: 3456; 3465; 3546; 3564; 3654; 3645 => 6 số x 4 cách đổi = 24 số
Số có 5 chữ số: 12456; 12465; 12564; 12546; 12645; 12654 => Số lượng: 6 x 4 x 5 = 120 số
Tổng thoả mãn: 4+18+24+120= 166(số)
18 tháng 1 2018
mk cho bài kham khảo nha :
có thể trở thành tử số mới.Và mỗi tử số mới có được ta đều tìm được mẫu số tương ứng.
Số có 2 chữ số nhỏ nhất chia hết cho 3 là 12 và số lớn nhất có 2 chữ số chia hết cho 3 là 99.
Số các phân số là: (99-12) : 3 + 1= 30 ( phân số)
:D
TH
18 tháng 1 2018
Bài tham khảo nè:
Với ba chữ số 1,2,3 thì có:
- Chữ số hàng trăm có 3 cách chọn
- Chữ số hàng chục có 3 cách chọn
- Chữ số hàng đơn vi cũng có 3 cách chọn
Vậy ta viết được các số có 3 chữ số là:
3 x 3 x 3 = 27 (số)
Với 0,1,2 thì có:
- Chữ số hàng trăm có 2 cách chọn ( Vì số 0 không thể đứng đầu được)
- Chữ số hàng chục có 3 cách chọn
- Chữ số hàng đơn vị có 3 cách chọn
Vậy ta viết được các số có 3 chữ số là:
2 x 3 x 3 = 18 (số)
17 tháng 5 2016
Ta có 1+2+3+4+5+6+ =21 Vậy tổng của 3 chữ số đầu là 10
Dễ thấy 1+3+6 = 1+4+5 = 2+3+5
Vậy có 3 cách chọn 3 nhóm 3 chữ số đầu (1,3,6 hoặc 1,4,5 hoặc 2,3,5)
Với 1 cách chọn nhóm 3 chữ số thì có 3! cách để lập ra số \(\overline{a_1a_2a_3}\)
Với 3 số còn lại thì có 3! cách để lập ra số \(\overline{a_4a_5a_6}\)
(ở đây \(\overline{a_1a_2a_3a_4a_5a_6}\) là số thỏa mãn yêu cầu đề ra)
Theo quy tắc nhân ta có 3.6.6 = 108
Vậy có 108 số cần tìm
TN
16 tháng 5 2020
Em thấy như này còn thiều trường hợp hay sao ý ạ tại ba số nhỏ hơn đâu nhất thiết phải bằng 10 ạ 123 vs 345 vẫn tỏa mãn đấy chứ ạ.Có thể cho em là mình sai ở đâu hay kế quả thế nào được không ạ??
CM
11 tháng 6 2017
Gọi 
là số cần lập a1 + a2 + a3 = 10
Theo bài ra ta có: 
(1)
Mà 
và đôi một khác nhau nên
a1,a2,a3,a4,a5,a6 = 1 + 2 + 3 + 4 + 5 + 6 =21
(2)
Từ (1), (2) suy ra: a1 + a2 + a3 = 10
Phương trình này có các bộ nghiệm là: ( a1 , a2 , a3 ) = (1,3,6); (1,4,5); (2,3,5)
Với mỗi bộ ta có 3!.3!=36 số.
Vậy có cả 3.36=108 số cần lập.
Chọn C.
CM
20 tháng 10 2017
Chọn đáp án C
Cách 1: Gọi x = a 1 a 2 . . . a 6 ¯ , a i ∈ 1 , 2 , 3 , 4 , 5 , 6 là số cần lập
Theo bài ra ta có:
Mà a 1 , a 2 , a 3 , a 4 , a 5 , a 6 ∈ 1 , 2 , 3 , 4 , 5 , 6 và đôi một khác nhau nên
Từ (1), (2) suy ra: a 1 + a 2 + a 3 = 10
Phương trình này có các bộ nghiệm là:
Với mỗi bộ ta có 36 số.
Vậy có cả thảy 3.36=108 số cần lập.
Cách 2: Gọi x = a b c d e f là số cần lập
Ta có:
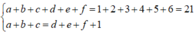
⇒ a + b + c = 11 .
Do a , b , c ∈ 1 , 2 , 3 , 4 , 5 , 6
Suy ra ta có các cặp sau:
Với mỗi bộ như vậy ta có 3! cách chọn a, b, c và 3! cách chọn d ,e ,f
Do đó: 3!.3!.3!= 108 số thỏa yêu cầu bài toán