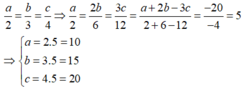Tìm a, b, c biết a=2b=\(\frac{3}{2}c\) và a2 + b3 - \(\sqrt{5^2}c\)=a + b3 -\(\frac{5}{3}c\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Nếu đề đúng.
\(a^2+b^3-\sqrt{5^2}c=a+b^3-\frac{5}{3}c\)
<=> \(a+\frac{10}{3}c=a^2\)
Mặt khác:
\(a=\frac{3}{2}c\)=> \(a=\frac{\frac{10}{3}c}{\frac{20}{9}.}=\frac{a+\frac{10}{3}c}{1+\frac{20}{9}}=\frac{a^2}{\frac{29}{9}}\)
=> \(\frac{29}{9}a=a^2\Leftrightarrow\orbr{\begin{cases}a=0\\a=\frac{29}{9}\end{cases}}\)
Với a=0 => b=c =0
Với \(a=\frac{29}{9}\Rightarrow b=\frac{29}{18};c=\frac{58}{27}\)

Ta có: 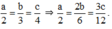
Theo tính chất dãy tỉ số bằng nhau ta có:
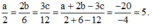
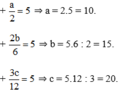
Vậy a = 10 ; b = 15 ; c = 20.

\(a,VT=\left(a^2+b^2\right)\left(c^2+d^2\right)=a^2c^2+b^2c^2+a^2d^2+b^2d^2\)
\(VP=\left(ac+bd\right)^2+\left(ad-bc\right)^2=a^2c^2+2abcd+b^2d^2+a^2d^2-2abcd+b^2c^2=a^2c^2+b^2c^2+a^2d^2+b^2d^2\)
\(\Rightarrow VT=a^2c^2+b^2c^2+a^2d^2+b^2d^2=VP\left(đpcm\right)\)
b, Tham khảo:Chứng minh hằng đẳng thức:(a+b+c)3= a3 + b3 + c3 + 3(a+b)(b+c)(c+a) - Hoc24

Bài 2: Mình nghĩ câu a là a+2b-3c=-20
a) Ta có: a/2 = b/3 = c/4 = 2b/6 = 3c/12 = a + 2b - 3c/ 2 + 6 - 12 = -20/-4 = 5
a/2 = 5 => a = 2 . 5 = 10
b/3 = 5 => b = 5 . 3 = 15
c/4 = 5 => c = 5 . 4 = 20
Vậy a = 10; b = 15; c = 20
b) Ta có: a/2 = b/3 => a/10 = b/15
b/5 = c/4 => b/15 = c/12
=> a/10 = b/15 = c/12 = a - b + c / 10 - 15 + 12 = -49/7 = -7
a/10 = -7 => a = -7 . 10 = -70
b/15 = -7 => b = -7 . 15 = -105
c/12 = -7 => c = -7 . 12 = -84
Vậy a = -70; b = -105; c = -84.