Hình thăng ABCD có S=218,7cm vuông;đáy béAB =4/5 đáy lớn CD và hiệu của chúng =3,6 cm.
a/Tính chiều cao hình thang ABCD
b/Tính S tam giác CBE,biết hai đường chéo AC và BD cắt nhau tại E
Mong các AE giúp đỡ,giúp được kết bạn và bái làm sư phụ luôn?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

vi hinh vuong mnpq co do dai canh gap 3 lan canh hinh vuong abcd nen sien h hinh vuong mnpq cung se gap len 3 lan
dien h hinh vuong mnpq la: 24*3=72

Chọn đáp án A
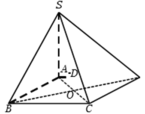
Đường chéo hình vuông AC = 2
Xét tam giác SAC, ta có
![]()
Chiều cao của khối chóp là SA = 3
Diện tích hình vuông ABCD là
![]()
Thể tích khối chóp S. ABCD là



* Chia hình vuông ABCD thành 4 hình vuông nhỏ có diện tích bằng nhau.( Vì hai cạnh kề với góc vuông bằng bán kình của hình tròn.)
* Diện tích mỗi hình vuông nhỏ la : 28 :4 = 7 ( cm2 )
- Mà diện tích mỗi hình vuông nhỏ bằng: r x r = 7 ( cm2 )
* Diện tích hình tròn là: r x r x 3,14 = 7 x 3,14 = 21,98 ( cm2 )
Đ/S: 21, 98 cm2.

a: ABCD là hình vuông
=>AB=BC=CD=DA và \(\widehat{DAB}=\widehat{ABC}=\widehat{BCD}=\widehat{ADC}=90^0\) và AC là phân giác của \(\widehat{DAB}\) và DB là phân giác của góc ADC; BD là phân giác của góc ABC
AC là phân giác của góc DAB
=>\(\widehat{CAB}=\dfrac{1}{2}\widehat{DAB}=\dfrac{1}{2}\cdot90^0=45^0\)
AEBF là hình vuông
=>AB là phân giác của \(\widehat{FAE}\) và \(\widehat{FAE}=90^0\)
=>\(\widehat{BAE}=\dfrac{1}{2}\cdot\widehat{EAF}=45^0\)
\(\widehat{BAE}=45^0\)
\(\widehat{BAC}=45^0\)
Do đó: \(\widehat{BAE}=\widehat{BAC}=45^0\)
=>AE và AC là hai tia trùng nhau
=>A,E,C thẳng hàng
BD là phân giác của góc ABC
=>\(\widehat{ABD}=\dfrac{\widehat{ABC}}{2}=\dfrac{90^0}{2}=45^0\)
AEBF là hình vuông
=>BA là phân giác của góc EBF
=>\(\widehat{ABE}=\dfrac{1}{2}\cdot\widehat{FBE}=45^0\)
=>\(\widehat{ABE}=\widehat{ABD}\)
=>BE,BD là hai tia trùng nhau
=>B,E,D thẳng hàng
B,E,D thẳng hàng
A,E,C thẳng hàng
Do đó: BD cắt AC tại E
ADCB là hình vuông
=>AC=BD và AC vuông góc với BD tại trung điểm của mỗi đường
=>AC vuông góc BD tại E và E là trung điểm chung của AC và DB
E là trung điểm của AC nên AC=2AE=2(cm)
E là trung điểm của BD nên BD=2EB=2(cm)
Xét tứ giác ADCB có DB\(\perp\)AC
nên \(S_{ADCB}=\dfrac{1}{2}\cdot DB\cdot AC=\dfrac{1}{2}\cdot2\cdot2=2\left(cm^2\right)\)
b: ADCB là hình vuông
=>\(S_{ADCB}=AB^2\)
=>\(AB^2=2\)
=>\(AB=\sqrt{2}\left(cm\right)\)
54cm2 đấy
Kết quả =54 cm vuông