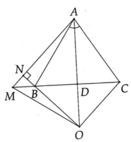
cho tam giác 0BC cân ở o trên tia đối của OC chứng minh AB<AC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TL
1
14 tháng 3 2016
bạn tự vẽ hình nhé:
xét tam giác AOB có: AB<AO+OB
Do A thuộc tia đối của tia 0C
=>A,O,C thẳng hàng .gọi đây là 1
tg OBC cân tại O.=>OB=OC gọi đây là 2
từ 1 và 2 =>AO+OB=AO+OC=AC
hay AB<AC(dpcm)
18 tháng 4 2020
Bài làm
a) Ta có: \(\widehat{OAB}+\widehat{OAP}=180^0\)( hai góc kề bù )
\(\widehat{OBA}+\widehat{MBD}=180^0\)( hai góc kề bù )
Mà \(\widehat{OAB}=\widehat{OBA}\)( Do tam giác OAB cân ở O )
=> \(\widehat{OAP}=\widehat{MBD}\)
Xét tam giác APC và tam giác BMD có:
AC = BD ( gt )
\(\widehat{OAP}=\widehat{MBD}\)( cmt )
PA = MB ( gt )
=> Tam giác APC = tam giác BMD ( c.g.c )
b) Vì tam giác APC = tam giác BMD ( cmt )
=> \(\widehat{DMB}=\widehat{CPA}\)
Mà \(\widehat{BMD}=\widehat{CMA}\)( Hai góc đối )
=> \(\widehat{CMA}=\widehat{CPA}\)
=> Tam giác CMP cân ở C
c) Vì tam giác CMP cân ở C
=> CP = CM ( hai cạnh bên )
Mà CP = MD ( do tam giác APC = tam giác BMD )
=> CM = MD
=> M là trung điểm CD ( đpcm )
1 tháng 9 2021
Xét ΔOAC và ΔODB có
\(\dfrac{OA}{OD}=\dfrac{OC}{OB}\)
\(\widehat{AOC}=\widehat{DOB}\)
Do đó: ΔOAC\(\sim\)ΔODB
Suy ra: \(\widehat{OCA}=\widehat{OBD}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AC//BD
Xét tứ giác ABDC có AC//BD
nên ABDC là hình thang