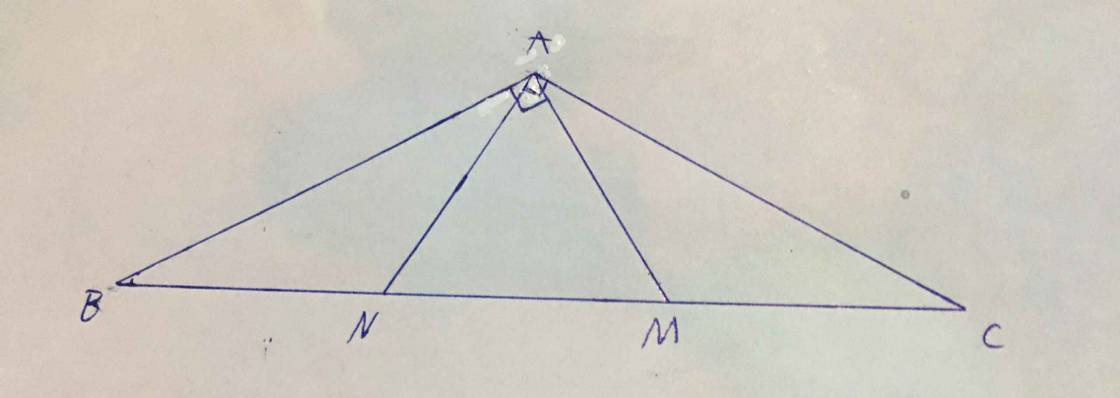
Câu 12. (3 điểm) Cho tam giác $ABC$ cân tại $A$ có $\widehat{A} = 120^{\circ}$. Trên cạnh $BC$ lấy hai điểm $M,$ $N$ sao cho $MA$, $NA$ lần lượt vuông góc với $AB$, $AC$. Chứng minh rằng:
a) $\Delta BAM = \Delta CAN$;
b) $BN = CM$;
c) $\Delta ANB$ cân tại $N$.

tam giác ABC cân tại A nên
\(\widehat{B}\) = \(\widehat{C}\)
=> \(\widehat{ABM}\) = \(\widehat{ACN}\) (1)
AB = AC (2)
\(\widehat{BAM}\) = \(\widehat{CAN}\) = 900 (3)
Kết hợp (1); (2); (3) ta có : Δ BAM = Δ CAN ( g-c-g)
=> BM = CN
BM = BN + MN = MN + CM
⇒ BN = CM
\(\widehat{BAN}\) + \(\widehat{NAC}\) = \(\widehat{BAC}\) = 1200
⇒ \(\widehat{BAN}\) = 1200 - \(\overline{NAC}\) = 1200 - 900 = 300
\(\widehat{ABN}\) = ( 1800 - 120 0 ) : 2 = 300 = \(\widehat{BAN}\) ⇒Δ ANB cân tại N