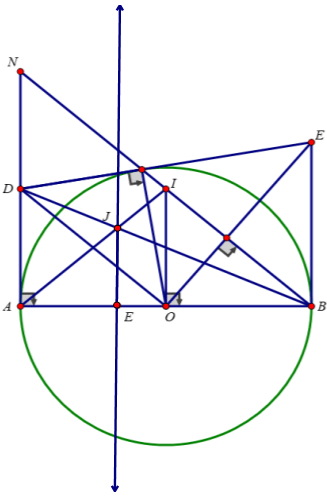
(3,5 điểm) Cho đường tròn $(O;R)$ và đường thẳng $d$ không có điểm chung với đường tròn. Từ điểm $M$ thuộc đường thẳng $d$ kẻ hai tiếp tuyến $MA$, $MB$ tới đường tròn. Hạ $OH$ vuông góc với đường thẳng $d$ tại $H$. Nối $AB$ cắt $OH$ tại $K$, cắt $OM$ tại $I$. Tia $OM$ cắt đường tròn $(O)$ tại $E$.
a) Chứng minh $AOBM$ là tứ giác nội tiếp.
b) Chứng minh $OI.OM=OK.OH$.
c) Chứng minh $E$ là tâm đường tròn nội tiếp tam giác $MAB$.
d) Tìm vị trí của $M$ trên đường thẳng $d$ để diện tích tam giác $OIK$ có giá trị lớn nhất.