12x2:3x2=
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: 3 x 2 + 2 x + 4 = 8 x 3 + 12 x 2 + 8 x + 1 3 x 2 + 2 x + 5 = ( 2 x + 1 ) 3 + 2 x + 1 3 x 2 + 2 x + 5 (1)
Dễ thấy 3 x 2 + 2 x + 4 > 0 với mọi x. Đặt u = 3 x 2 + 2 x + 4 v = 2 x + 1 .
Ta có: ( 1 ) ⇔ u = v 3 + v u 2 + 1 ⇔ u 3 + u = v 3 + v ⇔ ( u − v ) ( u 2 + u v + v 2 + 1 ) = 0 ⇔ u = v
(Vì u 2 + u v + v 2 + 1 = u + v 2 2 + 3 4 v 2 + 1 > 0 )
u = v ⇔ 3 x 2 + 2 x + 4 = 2 x + 1 ⇒ 3 x 2 + 2 x + 4 = 4 x 2 + 4 x + 1 x 2 − 2 x − 3 = 0 ⇒ x = 3 h o a c x = − 1.
Thử lại, ta nhận x= 3

Cả ba phương trình trên đều là phương trình trùng phương.
a) 3 x 4 – 12 x 2 + 9 = 0 ( 1 )
Đặt x 2 = t , t ≥ 0.
(1) trở thành: 3 t 2 – 12 t + 9 = 0 ( 2 )
Giải (2):
Có a = 3; b = -12; c = 9
⇒ a + b + c = 0
⇒ (2) có hai nghiệm t 1 = 1 v à t 2 = 3 .
Cả hai nghiệm đều thỏa mãn điều kiện.
+ t = 3 ⇒ x 2 = 3 ⇒ x = ± 3 + t = 1 ⇒ x 2 = 1 ⇒ x = ± 1
Vậy phương trình có tập nghiệm 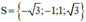
b) 2 x 4 + 3 x 2 – 2 = 0 ( 1 )
Đặt x 2 = t , t ≥ 0.
(1) trở thành: 2 t 2 + 3 t – 2 = 0 ( 2 )
Giải (2) :
Có a = 2 ; b = 3 ; c = -2
⇒ Δ = 3 2 – 4 . 2 . ( - 2 ) = 25 > 0
⇒ (2) có hai nghiệm
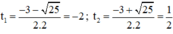
t 1 = - 2 < 0 nên loại.
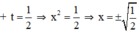
Vậy phương trình có tập nghiệm 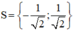
c) x 4 + 5 x 2 + 1 = 0 ( 1 )
Đặt x 2 = t , t > 0 .
(1) trở thành: t 2 + 5 t + 1 = 0 ( 2 )
Giải (2):
Có a = 1; b = 5; c = 1
⇒ Δ = 5 2 – 4 . 1 . 1 = 21 > 0
⇒ Phương trình có hai nghiệm:
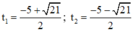
Cả hai nghiệm đều < 0 nên không thỏa mãn điều kiện.
Vậy phương trình (1) vô nghiệm.

a: =(x-1)^3
b: =(-2x+1)^3
c: =x^3-3x^2y+3xy^2-y^3
=(x-y)^3
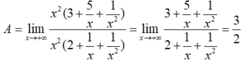
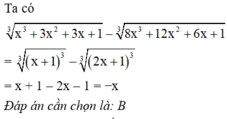
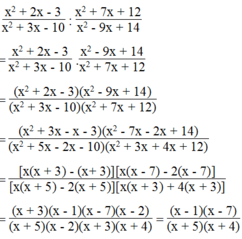

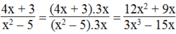
= 16 nha bn
12 x 2 : 3 x 2
= 24 : 3 x 2
= 8 x 2
= 16