Cho tg ABC vuông tại A, cs trọng tâm G(-1,2) và đt AB: x + 3y - 15=0, viết pt BC, bt D thuộc đg trung tuyến đi qua B
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


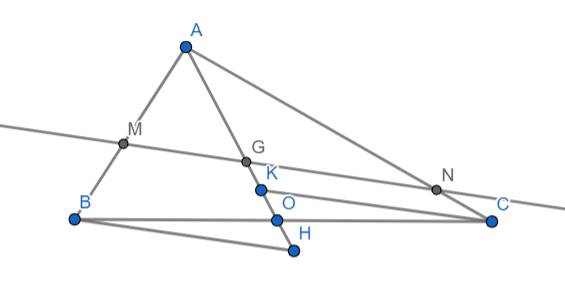
Xét 2 tam giác AMG và ABH ta có:
\(\widehat{BAH}\) chung
\(\widehat{AMG}=\widehat{ABH}\) (cặp góc đồng vị do BH//MG)
\(\Rightarrow\Delta AMG\sim\Delta ABH\left(g.g\right)\)
\(\Rightarrow\dfrac{AB}{AM}=\dfrac{AH}{AG}\) (1)
Xét 2 tam giác ANG và ACK có:
\(\widehat{CAK}\) chung
\(\widehat{ANG}=\widehat{ACK}\) (cặp góc đồng vị do CK//GN)
\(\Rightarrow\Delta ANG\sim\Delta ACK\left(g.g\right)\)
\(\Rightarrow\dfrac{AC}{AN}=\dfrac{AK}{AG}\) (2)
Xét hai tam giác BOH và COK ta có:
\(\widehat{BOH}=\widehat{COK}\) (đối đỉnh)
\(BO=CO\) (AO là đường trung tuyến nên O là trung điểm của BC)
\(\widehat{HBO}=\widehat{KCO}\) (so le trong vì BH//MN và CK//MN ⇒ BH//CK)
\(\Rightarrow\Delta BOH=\Delta COK\left(g.c.g\right)\)
\(\Rightarrow HO=OK\) (hai cạnh t.ứng)
\(\Rightarrow HK=2HO\)
Ta lấy (1) + (2) \(\Rightarrow\dfrac{AB}{AM}+\dfrac{AC}{AN}=\dfrac{AH+AK}{AG}=\dfrac{AH+AH+HK}{AG}=\dfrac{2AH+HK}{AG}\)
\(=\dfrac{2AH+2HO}{AG}=\dfrac{2\left(AH+HO\right)}{AG}=\dfrac{2AO}{AG}\)
Mà G là trọng tâm của tam giác ABC \(\Rightarrow AO=\dfrac{3}{2}AG\)
\(\Rightarrow\dfrac{AB}{AM}+\dfrac{AC}{AN}=\dfrac{2\cdot\dfrac{3}{2}AG}{AG}=2\cdot\dfrac{3}{2}=3\left(đpcm\right)\)

2. gọi E;F lần lượt là trung điểm của AB;AC
Xét tam giác MZT có AB//ZT ; mà E là trung điểm của AB
==> C là trung điểm của ZT ==> CT=CZ
tương tự BX=BY
MẶT KHÁC THEO CÂU a ta có AB.CZ=AC.BX
==> AB.CT=AC.BY<=> AB/BY=AC/CT <=> AB/AC=BY/CT
XÉT tam giác ABY và ACT đồng dạng theo (c.g.c)
=> góc BAY =góc CAT
DO ĐÓ MAB=NAC ( CÙNG CỘNG VS 2 GÓC ĐỐI ĐỈNH )

9/ \(\Delta//\left(d\right)\Rightarrow\overrightarrow{n_d}=\left(1;-2\right)\)
\(\Rightarrow\left(d\right):\left(x-1\right)-2\left(y+1\right)=0\)
\(\left(d\right):x-2y-3=0\)
10/ \(\overrightarrow{BC}=\left(-6;8\right)\)
PT đường cao AA' nhận vecto BC làm vtpt
\(\Rightarrow\overrightarrow{n_{AA'}}=\overrightarrow{u_{BC}}=\left(-6;8\right)\)
\(AA':-6\left(x-1\right)+8\left(y+2\right)=0\)
\(AA'=-6x+8y+22=0\)
18/ Trong quá trình làm bài, mình rút ra kết luận sau: Nếu một đường thẳng chắn 2 trục toạ độ 2 đoạn có độ dài bằng nhau thì ptđt có hệ số góc là \(k=\pm1\)
Để mình chứng minh lại:
Đường thẳng có dạng : y= ax+b
\(\Rightarrow\) Nó cắt trục Oy tại điểm có toạ độ là \(\left(0;b\right)\)
Và cắt trục Ox tại điểm có toạ độ là \(\left(-\frac{b}{a};0\right)\)
Vì khoảng cách từ O đến từng điểm là như nhau
\(\Rightarrow\left|b\right|=\left|\frac{b}{a}\right|\Leftrightarrow\left[{}\begin{matrix}b=\frac{b}{a}\\b=-\frac{b}{a}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}a=1\\a=-1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\overrightarrow{u}=\left(1;1\right)\\\overrightarrow{u}=\left(1;-1\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\left(d\right):x-2+y+3=0\\\left(d\right):x-2-y-3=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}\left(d\right):x+y+1=0\\\left(d\right):x-y-5=0\end{matrix}\right.\)