Cho tam giác ABC có BC = 2 BA, M là trung điểm của BC, BD là đường phân giác của tam giác ABC. Hai tia BA và MD cắt nhau tại E.
a) CM: Tam giác BDA = Tam giác BDM
b) CM: Tam giác BAC = Tam giác BME
c) Điểm D là gì của tam giác BCE? So sánh DC và DA
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 8 2023
a: Xét ΔBAD và ΔBMD có
BA=BM(=BC/2)
góc ABD=góc MBD
BD chung
=>ΔBAD=ΔBMD
b: ΔBAD=ΔBMD
=>góc BAD=góc BMD và BA=BM
Xét ΔBME và ΔBAC có
góc BME=góc BAC
BM=BA
góc MBE chung
=>ΔBME=ΔBAC
c: ΔBME=ΔBAC
=>BE=BC
=>BE=2BA
=>A là trung điểm của BE
Xét ΔBEC có
CA,EM là trung tuyến
CA cắt EM tại D
=>D là trọng tâm
=>CD=2DA
24 tháng 3 2017
Ngày mai mình nộp bài rồi, mong các bạn chỉ bài giúp mình . mình không hiểu gì về 2 bài toán này cả TT_TT
13 tháng 2 2016
Bạn tự vẽ hình nha
a) Cét 2 tam giác ABD VÀ ACD ta có :
AB = AC ( vì tam giác ABC cân )
góc A1 = A2 ( vì AD là tia pg của góc BAC )
AD là cạnh chung
= > tam giác ABD = ACD ( c.g.c )
b) Vì tg ABD = ACD ( cmt )
=> góc D1 = D2 ( 2 góc tương ứng )
mà D1 và D2 là 2 góc kề bù
= > góc D1 + D2 = 180 độ
mà D1 = D2
=> D1= D2= 180 độ : 2 = 90 độ
=>AD vuông góc với BC
c) Vì MD song song với AC
=> D1 = góc C ( 2 góc đồng vị )
mà góc B=C
=> B = D1
=> Tg MBD cân tại M
=> MB = MD
Câu d bạn tự làm nha
14 tháng 2 2016
Bạn tự vẽ hình nha
a) Cét 2 tam giác ABD VÀ ACD ta có :
AB = AC ( vì tam giác ABC cân )
góc A1 = A2 ( vì AD là tia pg của góc BAC )
AD là cạnh chung
= > tam giác ABD = ACD ( c.g.c )
b) Vì tg ABD = ACD ( cmt )
=> góc D1 = D2 ( 2 góc tương ứng )
mà D1 và D2 là 2 góc kề bù
= > góc D1 + D2 = 180 độ
mà D1 = D2
=> D1= D2= 180 độ : 2 = 90 độ
=>AD vuông góc với BC
c) Vì MD song song với AC
=> D1 = góc C ( 2 góc đồng vị )
mà góc B=C
=> B = D1
=> Tg MBD cân tại M
=> MB = MD
Câu d bạn tự làm nha
CH
Cô Hoàng Huyền
Admin
VIP
28 tháng 2 2018
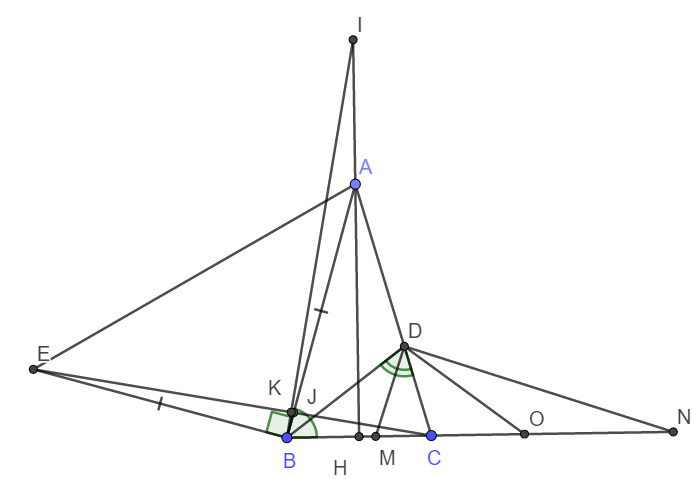
a)
+) Do tam giác ABC cân tại A nên trung tuyến AH đồng thời là đường caio.
Vậy nên \(\widehat{AHB}=90^o\)
Theo tính chất góc ngoài của tam giác, ta có:
\(\widehat{IAB}=\widehat{AHB}+\widehat{HBA}=90^o+\widehat{HBA}=\widehat{EBA}+\widehat{HBA}=\widehat{CBE}\)
Xét tam giác ABI và tam giác BEC có:
AI = BC (gt)
BA = EB (gt)
\(\widehat{IAB}=\widehat{CBE}\) (cmt)
\(\Rightarrow\Delta ABI=\Delta BEC\left(c-g-c\right)\)
+) Gọi giao điểm của EC với AB và BI lần lượt là J và K.
Do \(\Delta ABI=\Delta BEC\Rightarrow\widehat{KBJ}=\widehat{BEK}\)
Vậy thì \(\widehat{KBJ}+\widehat{KJB}=\widehat{BEK}+\widehat{KJB}=90^o\)
Suy ra \(\widehat{BKJ}=90^o\) hay \(BI\perp CE\)
b) Gọi O là trung điểm MN. Ta thấy DN và DM là phân giác của hai góc kề bù nên chúng vuông góc với nhau.
Vậy tam giác DMN vuông tại D. Khi đó ta có DO là trung tuyến ứng với cạnh huyền nên DO = MN/2
Vậy DO = OM = OM hay các tam giác DOM và DON cân tại O.
Ta có: \(\widehat{DOM}=180^o-2\widehat{DMO}=180^o-2\left(\widehat{MDB}+\widehat{MBD}\right)\)
\(=180^o-2.\widehat{MDB}-2.\widehat{MBD}=180^o-\widehat{BDC}-\widehat{ABC}\)
\(=180^o-\widehat{BDC}-\widehat{ACB}=\widehat{DBO}\)
Vậy tam giác DBO cân tại D hay DB = DO.
Vậy nên BD = MN/2.
25 tháng 8 2018
xét tam giác BAI va CBE
be=ab
bc=ia
iab=ebc
=>tam giác BAI=tam giác CBE
khó quá
CM là gì