Tìm x,y nguyên: x2y2-xy=x2+2y2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 1 2024
a.
\(\Leftrightarrow2x^2-4x+4y^2=4xy+4\)
\(\Leftrightarrow\left(x^2-4xy+4y^2\right)+\left(x^2-4x+4\right)=8\)
\(\Leftrightarrow\left(x-2y\right)^2+\left(x-2\right)^2=8\) (1)
Do \(\left(x-2y\right)^2\ge0;\forall x;y\)
\(\Rightarrow\left(x-2\right)^2\le8\)
\(\Rightarrow\left(x-2\right)^2=\left\{0;1;4\right\}\)
TH1: \(\left(x-2\right)^2\Rightarrow x=2\) thế vào (1)
\(\Rightarrow\left(2-2y\right)^2=8\Rightarrow\left(1-y\right)^2=2\) (ko tồn tại y nguyên t/m do 2 ko phải SCP)
TH2: \(\left(x-2\right)^2=1\Rightarrow\left(x-2y\right)^2=8-1=7\), mà 7 ko phải SCP nên pt ko có nghiệm nguyên
TH3: \(\left(x-2\right)^2=4\Rightarrow\left[{}\begin{matrix}x=4\\x=0\end{matrix}\right.\) thế vào (1):
- Với \(x=0\Rightarrow\left(-2y\right)^2+4=8\Rightarrow y^2=1\Rightarrow y=\pm1\)
- Với \(x=2\Rightarrow\left(2-2y\right)^2+4=8\Rightarrow\left(1-y\right)^2=1\Rightarrow\left[{}\begin{matrix}y=0\\y=2\end{matrix}\right.\)
Vậy pt có các cặp nghiệm là:
\(\left(x;y\right)=\left(0;1\right);\left(0;-1\right);\left(2;0\right);\left(2;2\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 1 2024
b.
\(\Leftrightarrow2x^2+4y^2+4xy-4x=14\)
\(\Leftrightarrow\left(x^2+4xy+4y^2\right)+\left(x^2-4x+4\right)=18\)
\(\Leftrightarrow\left(x+2y\right)^2+\left(x-2\right)^2=18\) (1)
Lý luận tương tự câu a ta được
\(\left(x-2\right)^2\le18\Rightarrow\left(x-2\right)^2=\left\{0;1;4;9;16\right\}\)
Với \(\left(x-2\right)^2=\left\{0;1;4;16\right\}\) thì \(18-\left(x-2\right)^2\) ko phải SCP nên ko có giá trị nguyên x;y thỏa mãn
Với \(\left(x-2\right)^2=9\Rightarrow\left[{}\begin{matrix}x=5\\x=-1\end{matrix}\right.\) thế vào (1)
- Với \(x=5\Rightarrow\left(5+2y\right)^2+9=18\Rightarrow\left(5+2y\right)^2=9\)
\(\Rightarrow\left[{}\begin{matrix}5+2y=3\\5+2y=-3\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}y=-1\\y=-4\end{matrix}\right.\)
- Với \(x=-1\Rightarrow\left(-1+2y\right)^2=9\Rightarrow\left[{}\begin{matrix}-1+2y=3\\-1+2y=-3\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}y=2\\y=-1\end{matrix}\right.\)
Vậy \(\left(x;y\right)=\left(5;-1\right);\left(5;-4\right);\left(-1;3\right);\left(-1;-3\right)\)
D
2
AH
Akai Haruma
Giáo viên
16 tháng 7 2021
Bạn vui lòng viết đề đầy đủ, và gõ bằng công thức toán để được hỗ trợ tốt hơn.
T
1
AH
Akai Haruma
Giáo viên
27 tháng 8 2023
Lời giải:
$x^2+2y^2+x^2y^2-10xy+16=0$
$\Leftrightarrow (x^2+y^2-2xy)+(x^2y^2-8xy+16)+y^2=0$
$\Leftrightarrow (x-y)^2+(xy-4)^2+y^2=0$
Vì $(x-y)^2\geq 0; (xy-4)^2\geq 0; y^2\geq 0$ với mọi $x,y$
$\Rightarrow$ để tổng của chúng bằng $0$ thì:
$(x-y)^2=(xy-4)^2=y^2=0$
$\Leftrightarrow x=y=0$ và $xy=4$ (vô lý)
Vậy không tồn tại $x,y$ thỏa mãn đề nên cũng không tồn tại $T$.
MP
0
NP
1
25 tháng 12 2020
\(\Leftrightarrow\left\{{}\begin{matrix}x^3+2y^2-4y+3=0\\2x^2+2x^2y^2-4y=0\left(1\right)\end{matrix}\right.\Rightarrow}x^3+2y^2-4y-2x^2-2x^2y^2+4y=0\Rightarrow x^3+1-2x^2y^2+2y^2-2x^2+2=0\Rightarrow\left(x+1\right)\left(x^2-x+1\right)-2y^2\left(x-1\right)\left(x+1\right)-2\left(x-1\right)\left(x+1\right)=0\Rightarrow\left(x+1\right)\left(x^2-x+1-2xy^2+2y^2-2x+2\right)=0\Rightarrow x=-1\)Thay x=-1 vào (1) ta được y2-2y+1=0⇒ (y-1)2=0⇒y-1=0⇒y=1
Do đó Q=x2+y2=(-1)2+12=2
TC
2
25 tháng 4 2017
\(x^2+2x^2y^2+2y^2-\left(x^2y^2+2x^2\right)-2=0\)
\(\Leftrightarrow x^2+2x^2y^2+2y^2-x^2y^2-2x^2-2=0\)
\(\Leftrightarrow x^2y^2-x^2+2y^2-2=0\)
\(\Leftrightarrow\left(x^2y^2-x^2\right)+\left(2y^2-2\right)=0\)
\(\Leftrightarrow x^2\left(y^2-1\right)+2\left(y^2-1\right)=0\)
\(\Leftrightarrow\left(x^2+2\right)\left(y^2-1\right)=0\)
\(\Leftrightarrow\left(x^2+2\right)\left(y-1\right)\left(y+1\right)=0\)
Dễ thấy: \(x^2+2\ge2>0\forall x\) (vô nghiệm)
\(\Rightarrow\left[{}\begin{matrix}y-1=0\\y+1=0\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}y=1\\y=-1\end{matrix}\right.\)
23 tháng 3 2017
2,
M + N = 3xyz - 3x2 + 5xy - 1 + 5x2 + xyz - 5xy + 3 - y
= -3x2 + 5x2 + 3xyz + xyz + 5xy - 5xy - y - 1 + 3
= 2x2 + 4xyz - y +2.
M - N = (3xyz - 3x2 + 5xy - 1) - (5x2 + xyz - 5xy + 3 - y)
= 3xyz - 3x2 + 5xy - 1 - 5x2 - xyz + 5xy - 3 + y
= -3x2 - 5x2 + 3xyz - xyz + 5xy + 5xy + y - 1 - 3
= -8x2 + 2xyz + 10xy + y - 4.
N - M = (5x2 + xyz - 5xy + 3 - y) - (3xyz - 3x2 + 5xy - 1)
= 5x2 + xyz - 5xy + 3 - y - 3xyz + 3x2 - 5xy + 1
= 5x2 + 3x2 + xyz - 3xyz - 5xy - 5xy - y + 3 + 1
= 8x2 - 2xyz - 10xy - y + 4.
3,
a) P + (x2 – 2y2) = x2 – y2 + 3y2 – 1
P = (x2 – y2 + 3y2 – 1) - (x2 – 2y2)
P = x2 – y2 + 3y2 – 1 - x2 + 2y2
P = x2 – x2 – y2 + 3y2 + 2y2 – 1
P = 4y2 – 1.
Vậy P = 4y2 – 1.
b) Q – (5x2 – xyz) = xy + 2x2 – 3xyz + 5
Q = (xy + 2x2 – 3xyz + 5) + (5x2 – xyz)
Q = xy + 2x2 – 3xyz + 5 + 5x2 – xyz
Q = 7x2 – 4xyz + xy + 5
Vậy Q = 7x2 – 4xyz + xy + 5.
4,
a, Thu gọn : x2+2xy-3x3+2y3+3x3-y3
= x2+2xy+(-3x3+3x3)+2y3-y3
=x2+2xy+2y3-y3
Thay x=5,y=4 vào đa thức x2+2xy+2y3-y3 Ta có:
52 + 2.5.4 + 43 = 25 + 40 + 64 = 129.
Vậy giá trị của đa thức x2+2xy+2y3-y3 tại x=5,y=4 là 129
b,
Thay x = -1; y = -1 vào biểu thức xy-x2y2+x4y4-x6y6+x8y8 Ta Có
M = (-1)(-1) - (-1)2.(-1)2 + (-1)4. (-1)4-(-1)6.(-1)6 + (-1)8.(-1)8
= 1 -1 + 1 - 1+ 1 = 1.
Vậy giá trị của biểu thức xy-x2y2+x4y4-x6y6+x8y8 tại x=-1, y=-1 là 1
5,
a, C=A+B
C = x2 – 2y + xy + 1 + x2 + y - x2y2 - 1
C = 2x2 – y + xy - x2y2
b) C + A = B => C = B - A
C = (x2 + y - x2y2 - 1) - (x2 – 2y + xy + 1)
C = x2 + y - x2y2 - 1 - x2 + 2y - xy - 1
C = - x2y2 - xy + 3y - 2.
TV
1
16 tháng 1 2021
Nếu x, y không chia hết cho 3 thì x2 chia cho 3 dư 1, do đó \(\left(x^2+2\right)^2\) chia hết cho 3.
Mà \(2y^4+11y^2+x^2y^2+9\) không chia hết cho 3 nên suy ra vô lí.
Do đó x = 3 hoặc y = 3 (Do x, y là các số nguyên tố).
Với x = 3 ta có \(2y^4+20y^2+9=121\Leftrightarrow y^4+10y^2-56=0\Leftrightarrow\left(y^2-4\right)\left(y^2+14\right)=0\Leftrightarrow y=2\) (Do y là số nguyên tố).
Với y = 3 ta có:
\(\left(x^2+2\right)^2=9x^2+270\Leftrightarrow x^4-5x^2-266=0\Leftrightarrow\left(x^2+14\right)\left(x^2-19\right)=0\). Không tồn tại số nguyên tố x thoả mãn.
Vậy x = 2; y = 3.
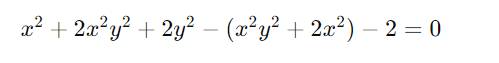
x=0
y=0