cho hình lập phương abcd và efgh cạnh a. Tính hđ vô hướng của 2 vecto sau a) vecto AC và vecto AF b) vecto DF và vecto EB
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a,\overrightarrow{AB}=\left(2;10\right)\)
\(\overrightarrow{AC}=\left(-5;5\right)\)
\(\overrightarrow{BC}=\left(-7;-5\right)\)
\(b,\) Thiếu dữ kiện
\(c,Cos\left(\overrightarrow{AB},\overrightarrow{AC}\right)=\dfrac{\left|2\left(-5\right)+10.5\right|}{\sqrt{2^2+10^2}.\sqrt{\left(-5\right)^2+5^2}}=\dfrac{2\sqrt{13}}{13}\)
\(\Rightarrow\left(\overrightarrow{AB},\overrightarrow{AC}\right)=56^o18'\)
\(Cos\left(\overrightarrow{AB},\overrightarrow{BC}\right)=\dfrac{\left|2\left(-7\right)+10\left(-5\right)\right|}{\sqrt{2^2+10^2}.\sqrt{\left(-7\right)^2+\left(-5\right)^2}}\)
\(\Rightarrow\left(\overrightarrow{AB},\overrightarrow{BC}\right)=43^o9'\)

1. Do \(EG||AC\Rightarrow\widehat{\left(\overrightarrow{AF};\overrightarrow{EG}\right)}=\widehat{\left(\overrightarrow{AF};\overrightarrow{AC}\right)}=\widehat{FAC}\)
Mà \(AF=AC=CF=AB\sqrt{2}\Rightarrow\Delta ACF\) đều
\(\Rightarrow\widehat{FAC}=60^0\)
2.
Do I;J lần lượt là trung điểm SC, BC \(\Rightarrow IJ\) là đường trung bình tam giác SBC
\(\Rightarrow IJ||SB\)
Lại có \(CD||BA\Rightarrow\widehat{\left(IJ;CD\right)}=\widehat{SB;BA}=\widehat{SBA}=60^0\) (do các cạnh của chóp bằng nhau nên tam giác SAB đều)

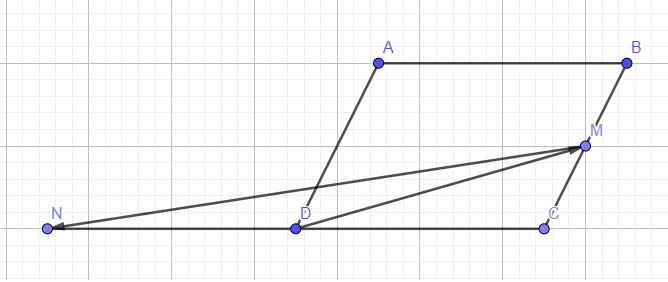
\(\overrightarrow{NC}=2\overrightarrow{ND}=2\overrightarrow{NC}+2\overrightarrow{CD}\Rightarrow\overrightarrow{NC}=2\overrightarrow{DC}\Rightarrow\overrightarrow{CN}=2\overrightarrow{CD}\)
a.
\(\overrightarrow{DM}=\overrightarrow{DC}+\overrightarrow{CM}=\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{CB}=\overrightarrow{AB}-\dfrac{1}{2}\overrightarrow{AD}\)
\(\overrightarrow{MN}=\overrightarrow{MC}+\overrightarrow{CN}=\dfrac{1}{2}\overrightarrow{BC}+2\overrightarrow{CD}=-2\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AD}\)
b.
\(\left\{{}\begin{matrix}\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}\\\overrightarrow{BD}=\overrightarrow{BA}+\overrightarrow{AD}=-\overrightarrow{AB}+\overrightarrow{AD}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\dfrac{1}{2}\overrightarrow{AC}-\dfrac{1}{2}\overrightarrow{BD}\\\overrightarrow{AD}=\dfrac{1}{2}\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{BD}\end{matrix}\right.\)
\(\Rightarrow\overrightarrow{MN}=-2\left(\dfrac{1}{2}\overrightarrow{AC}-\dfrac{1}{2}\overrightarrow{BD}\right)+\dfrac{1}{2}\left(\dfrac{1}{2}\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{BD}\right)=-\dfrac{3}{4}\overrightarrow{AB}+\dfrac{5}{4}\overrightarrow{BD}\)

\(\overrightarrow{AF}=\overrightarrow{AE}+\overrightarrow{AB}\)
\(\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}\)
\(\overrightarrow{AH}=\overrightarrow{AE}+\overrightarrow{AD}\)
\(\Rightarrow\overrightarrow{AF}-\overrightarrow{AC}+\overrightarrow{AH}=\overrightarrow{AE}+\overrightarrow{AB}-\overrightarrow{AB}-\overrightarrow{AD}+\overrightarrow{AE}+\overrightarrow{AD}\)
\(\Rightarrow\overrightarrow{AE}=\dfrac{1}{2}\overrightarrow{AF}-\dfrac{1}{2}\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{AH}\)