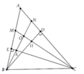
Cho tam giác ABC nhọn có BD và CE là 2 đường cao cắt nhau tại H (AB<AC) có ED cắt BC tại I. Chứng minh EC là phân giác của góc DEF( với F là giao điểm của AH và BC)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
góc DAB chung
=>ΔADB đồng dạng với ΔAEC
=>AD/AE=AB/AC
=>AD/AB=AE/AC
=>ΔADE đồng dạng vơi ΔABC
b: Xet ΔHEB vuông tại E và ΔHDC vuông tại D co
góc EHB=góc DHC
=>ΔHEB đồng dạng vơi ΔHDC
=>HE/HD=HB/HC
=>HE*HC=HB*HD
Xét tứ giác BHCK co
BH//CK
BK//CH
=>BHCK là hình bình hành
=>BC cắt HK tại trung điểm của mỗi đường
=>H,M,K thẳng hàng
ΔAED đồg dạng với ΔACB
=>góc AED=góc ACB
d: Xét ΔBEC vuông tại E và ΔBOA vuông tại O có
góc EBC chung
=>ΔBEC đồng dạng với ΔBOA
=>BE/BO=BC/BA
=>BE*BA=BO*BC
Xét ΔCDB vuông tại D và ΔCOA vuông tại O có
góc OCA chung
=>ΔCDB đồng dạng với ΔCOA
=>CD/CO=CB/CA
=>CO*CB=CD*CA
=>BE*BA+CD*CA=BC^2

a) Sử dụng tính chất tổng các góc trong một tam giác bằng 1800.
⇒ A B C ^ = A E C ^ ⇒ N B D ^ = M C A ^
Trong DDBN có: N B D ^ + B N D ^ = 90 0
Gọi O = CM Ç BN Þ CM ^ BN = O (1)
b) Xét DCNK có: CO ^ KN Þ CO ^ BN, CO là phân giác A C E ^ nên DCNK cân ở C Þ O là trung điểm KN (2).
Tương tự chứng minh được là trung điểm MH (3).
Từ (1),(2) và (3) suy ra MNHK là hình thoi.