So sánh \(\dfrac{3}{4}+\dfrac{3}{9}+\dfrac{3}{16}+...+\dfrac{3}{\left(3n\right)^2}\) với 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(A=\left(\dfrac{1}{2}-1\right)\left(\dfrac{1}{3}-1\right)\cdot...\cdot\left(\dfrac{1}{10}-1\right)\)
\(=\dfrac{-1}{2}\cdot\dfrac{-2}{3}\cdot...\cdot\dfrac{-9}{10}\)
\(=-\dfrac{1}{10}\)
9<10
=>1/9>1/10
=>\(-\dfrac{1}{9}< -\dfrac{1}{10}\)
=>\(A>-\dfrac{1}{9}\)
b: \(B=\left(\dfrac{1}{4}-1\right)\left(\dfrac{1}{9}-1\right)\cdot...\cdot\left(\dfrac{1}{100}-1\right)\)
\(=\left(\dfrac{1}{2}-1\right)\left(\dfrac{1}{3}-1\right)\cdot...\cdot\left(\dfrac{1}{10}-1\right)\left(\dfrac{1}{2}+1\right)\left(\dfrac{1}{3}+1\right)\cdot...\cdot\left(\dfrac{1}{10}+1\right)\)
\(=\dfrac{-1}{2}\cdot\dfrac{-2}{3}\cdot...\cdot\dfrac{-9}{10}\cdot\dfrac{3}{2}\cdot\dfrac{4}{3}\cdot...\cdot\dfrac{11}{10}\)
\(=\dfrac{-1}{10}\cdot\dfrac{11}{2}=\dfrac{-11}{20}\)
20<21
=>\(\dfrac{11}{20}>\dfrac{11}{21}\)
=>\(-\dfrac{11}{20}< -\dfrac{11}{21}\)
=>\(B< -\dfrac{11}{21}\)

Biểu thức thứ nhất
\(\dfrac{8}{5}:\dfrac{6}{5}=\dfrac{8}{6}=\dfrac{4}{3}\)
Biểu thức thứ hai:
\(\dfrac{5}{3}-\dfrac{5}{3}=0\)
Vậy biểu thức thứ nhất lớn hơn biểu thức thứ 2

11) \(\dfrac{5}{7}\left(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{4}{7}\right)+\left(\dfrac{1}{3}-\dfrac{1}{2}-\dfrac{4}{7}\right):\dfrac{7}{5}\)
= \(\dfrac{5}{7}\left(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{4}{7}\right)+\left(\dfrac{1}{3}-\dfrac{1}{2}-\dfrac{4}{7}\right)\cdot\dfrac{5}{7}\)
= \(\dfrac{5}{7}\left(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{4}{7}+\dfrac{1}{3}-\dfrac{1}{2}-\dfrac{4}{7}\right)\)
= \(\dfrac{5}{7}\cdot0\)
=0
12) \(\dfrac{43}{5}\left(\dfrac{17}{3}-\dfrac{16}{9}+2\right)-\dfrac{43}{5}\left(\dfrac{17}{3}-\dfrac{16}{9}\right)\)
= \(\dfrac{43}{5}\left(\dfrac{17}{3}-\dfrac{16}{9}+2-\dfrac{17}{3}+\dfrac{16}{9}\right)\)
= \(\dfrac{43}{5}\cdot2=\dfrac{43}{10}\)
11, 5/7( 1/2-1/3+1/4)+ (1/3-1/2-1/4):7/5
= 5/7.(1/2 - 1/3 + 1/4 )+( 1/3 - 1/2 - 1/4). 5/7
= 5/7.(1/2 - 2/3 + 1/4 + 1/3 - 1/2 - 1/4)
= 5/7 . -1/3
= -5/21
12, 43/5.(17/3 - 16/9 + 2)- 43/5. (17/3 - 16/9)
= 43/5.( 17/3 - 16/9 + 2 - 17/3 + 16/9)
= 43/5 . 2
= 86/5

a: \(=\dfrac{-3}{4}\left(31+\dfrac{11}{23}+8+\dfrac{12}{23}\right)=\dfrac{-3}{4}\cdot40=-30\)
b: \(=\left(\dfrac{7}{3}+\dfrac{7}{2}\right):\left(-\dfrac{25}{6}+\dfrac{22}{7}\right)+\dfrac{15}{2}\)
\(=\dfrac{35}{6}:\dfrac{-175+132}{42}+\dfrac{15}{2}\)
\(=\dfrac{35}{6}\cdot\dfrac{42}{-43}+\dfrac{15}{2}\)
\(=\dfrac{35\cdot7}{-43}+\dfrac{15}{2}\)
\(=\dfrac{-70\cdot7+15\cdot43}{86}=\dfrac{155}{86}\)
c: \(=\dfrac{-7}{5}\left(4+\dfrac{5}{9}+5+\dfrac{4}{9}\right)=\dfrac{-7}{5}\cdot10=-14\)
d: \(=4+\dfrac{25}{16}+25\cdot\left(\dfrac{9}{16}\cdot\dfrac{64}{125}\cdot\dfrac{-8}{27}\right)\)
\(=\dfrac{89}{16}+25\cdot\dfrac{-32}{375}\)
\(=\dfrac{89}{16}-\dfrac{32}{15}=\dfrac{823}{240}\)
e: \(=\dfrac{2}{3}-4\cdot\left(\dfrac{2}{4}+\dfrac{3}{4}\right)=\dfrac{2}{3}-5=-\dfrac{13}{3}\)
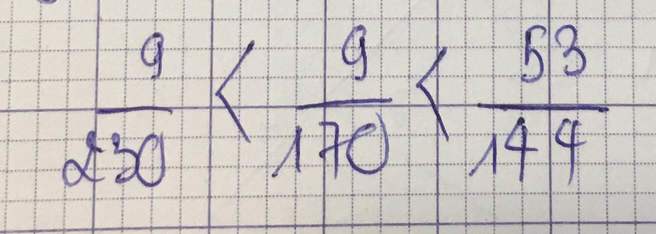
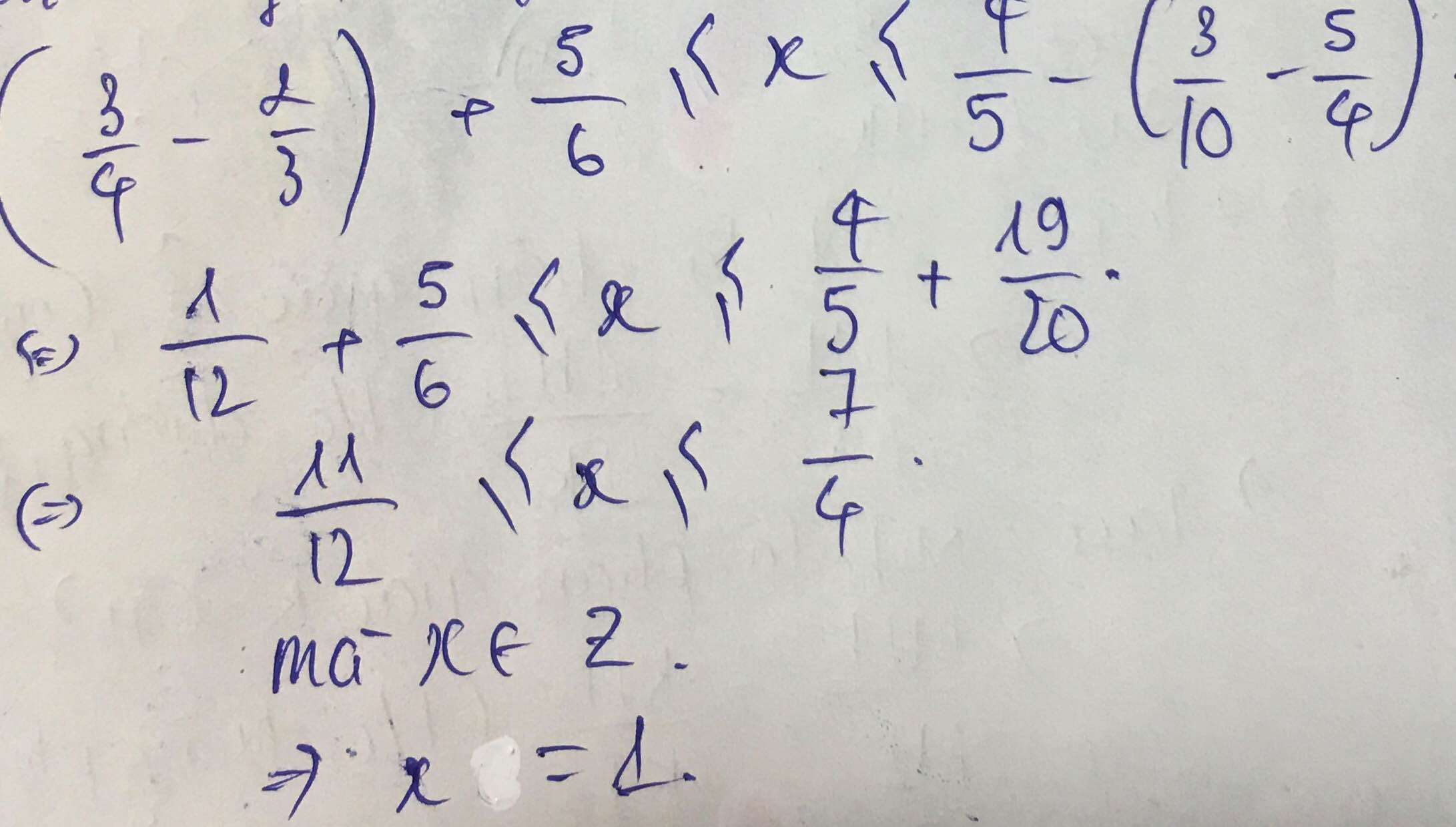
A = \(\dfrac{3}{4}\) + \(\dfrac{3}{9}\) + \(\dfrac{3}{16}\) + \(\dfrac{3}{25}\) +..............+ \(\dfrac{3}{(3n)^2}\)
A = ( \(\dfrac{3}{4}\) + \(\dfrac{3}{9}\) + \(\dfrac{3}{16}\)+ \(\dfrac{3}{25}\)) +.....+ \(\dfrac{3}{(3n)^2}\)
A = 3. ( \(\dfrac{1}{2^2}\) + \(\dfrac{1}{3^2}\) + \(\dfrac{1}{4^2}\) + \(\dfrac{1}{5^2}\))+............+ \(\dfrac{3}{(3n)^2}\)
A = 3.( \(\dfrac{1}{2.2}\) + \(\dfrac{1}{3.3}\) + \(\dfrac{1}{4.4}\) + \(\dfrac{1}{5.5}\)) +............+ \(\dfrac{3}{(3n)^2}\)
Vì \(\dfrac{1}{2}\) > \(\dfrac{1}{3}\) > \(\dfrac{1}{4}\) > \(\dfrac{1}{5}\)Ta có : \(\dfrac{1}{2.2}>\dfrac{1}{2.3}>\dfrac{1}{3.3}>\dfrac{1}{3.4}>\dfrac{1}{4.4}>\dfrac{1}{4.5}>\dfrac{1}{5.5}>\dfrac{1}{5.6}\)
A > 3. ( \(\dfrac{1}{2.3}\) + \(\dfrac{1}{3.4}\) + \(\dfrac{1}{4.5}\) + \(\dfrac{1}{5.6}\)) + ............+ \(\dfrac{1}{(3n)^2}\)
A > 3. ( \(\dfrac{1}{2}\) - \(\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}\)) +.....+ \(\dfrac{1}{(3n)^2}\)
A > 3.( \(\dfrac{1}{2}\) - \(\dfrac{1}{6}\)) +..............+ \(\dfrac{1}{(3n)^2}\)
A > 3. \(\dfrac{1}{3}\) +...............+ \(\dfrac{1}{(3n)^2}\)
A > 1 +..........+ \(\dfrac{1}{9n^2}\) > 1
A > 1