Giả sử 2 đường trung tuyến BD và CE của tam giác ABC có độ dài bằng nhau và cắt nhau ở G.
a) Tam giác BGC là tam giác gì?
b) So sánh tam giác BCD và tam giác CBE
c) Tam giác ABC là tam giác gì?
Ai trả lời sớm nhất và đúng nhất mình tích cho .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 4 2018
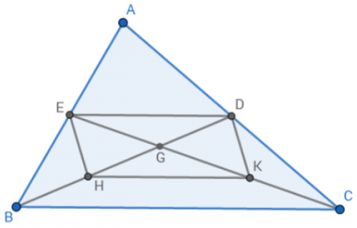
a)
BD là đường trung tuyến của Δ ABC nên D là trung điểm của AC (1)
CE là đường trung tuyến của Δ ABC nên E là trung điểm của AB (2)
Từ (1) và (2) suy ra :
DE là đường trung bình của Δ ABC
=> DE // BC và DE = 1/2 BC
Δ BGC có H là trung điểm của GB và K là trung điểm của GC
suy ra HK là đường trung bình của Δ BGC
=> HK // BC và HK = 1/2 BC
Tứ giác DEHK có DE//BC, HK // BC và DE = HK = 1/2 BC
nên tứ giác
b) DEHK là hình bình hành nên
HG = GD = 1/2 HD và GE = GK = 1/2 EK
Để tứ giác DEHK là hình chữ nhật thì
HD = EK => 1/2 HD = 1/2 EK => GE = GD và GH = GK
GH = GK => 2GH = 2GK => GB = GC
Xét Δ GEB và Δ GDC có
GE = GD Góc EGB = góc DGC GB = GC => ΔGEB = ΔGDC (c.g.c) => BE = CD => 2BE = 2CD => AB = AC => ΔABC cân tại A Vậy đểtứ giác DEHK là hình chữ nhật thì
ΔABC cân tại Ac) BD ⊥ CE => HD ⊥ EK Hình bình hành DEHK có HD ⊥ EK nên DEHK là hình thoi Vậy
nếu các đường trung tuyến BD và CE vuông góc với nhau thì tứ giác DEHK là hình thoi
8 tháng 4 2023
a: Gọi H là trung điểm của AE
=>AH=HE=EB
Xét ΔAEC có AH/AE=AD/AC
nên HD//EC và HD=1/2EC
Xét ΔBHD có BE/BH=BG/BD
nên EG//HD và EG=1/2HD
=>EG=1/4EC
=>EG=1/3GC
\(S_{ABG}=3\cdot S_{GEB}\)(Vì AB=3*BE)
\(S_{GBC}=3\cdot S_{GEB}\)
=>\(S_{ABG}=S_{BGC}\)
b: EG=1/3GC
22 tháng 4 2023
a: Xet ΔHEB vuông tại E và ΔHDC vuông tại D có
góc EHB=góc DHC
=>ΔHEB đồng dạng với ΔHDC
b: góc BEC=góc BDC=90 độ
=>BEDC nội tiếp
=>góc DEC=góc DBC
c: ΔEBC vuông tại E
mà EO là trung tuyến
nên EO=BC/2
ΔDBC vuông tại D
mà DO là trung tuyến
nên DO=BC/2=EO
=>ΔDOE cân tại O
a,Ta có: \(BD=CE\Rightarrow\frac{2}{3}BD=\frac{2}{3}CE\Rightarrow BG=CG.\)
Vậy tam giác BCG là tam giác cân tại G.
b, Ta có: \(\hept{\begin{cases}BD=CE\\BG=CG\end{cases}\Rightarrow BD-BG=CE-CG\Rightarrow GD=GE.}\)
Xét \(\Delta BGE\) và \(\Delta CGD:\)
\(\hept{\begin{cases}GD=GE\left(cmt\right)\\\widehat{BGE}=\widehat{CGD}\\BG=CG\left(cmt\right)\end{cases}\Rightarrow\Delta BGE=\Delta CGD\left(c.g.c\right)}\)
\(\Rightarrow BE=CD\)
Xét \(\Delta BCD\) và \(\Delta CDE:\)
\(\hept{\begin{cases}BC:chung\\BE=CD\left(cmt\right)\\BD=CE\left(gt\right)\end{cases}\Rightarrow\Delta BCD=\Delta CDE\left(c.c.c\right)}\)
c, Ta có: \(\Delta BCD=\Delta CDE\left(cmt\right)\Rightarrow\widehat{ABC}=\widehat{ACB}\)
Vậy tam giác ABC là tam giác cân tại A.
GIúp mình đi ngày mai mình phải nộp bài rồi TT_TT