Cho tam giác nhọn ABC AB < BC< AC nội tiếp trong đường tròn (O), Kẻ đường cao AD, BE, CF cắt nhau tại H.
1. Chứng minh tứ giác CDHE nội tiếp đường tròn đường kính HC
2. Đường tròn (K) đường kính HC cắt đường tròn (O) ở M ( M khác C). B< cắt đường tròn (K) ở N. Chứng minh BD.BC = BN.BM
3. CM AB// EN
4. 3 điểm N,D, F thẳng hàng

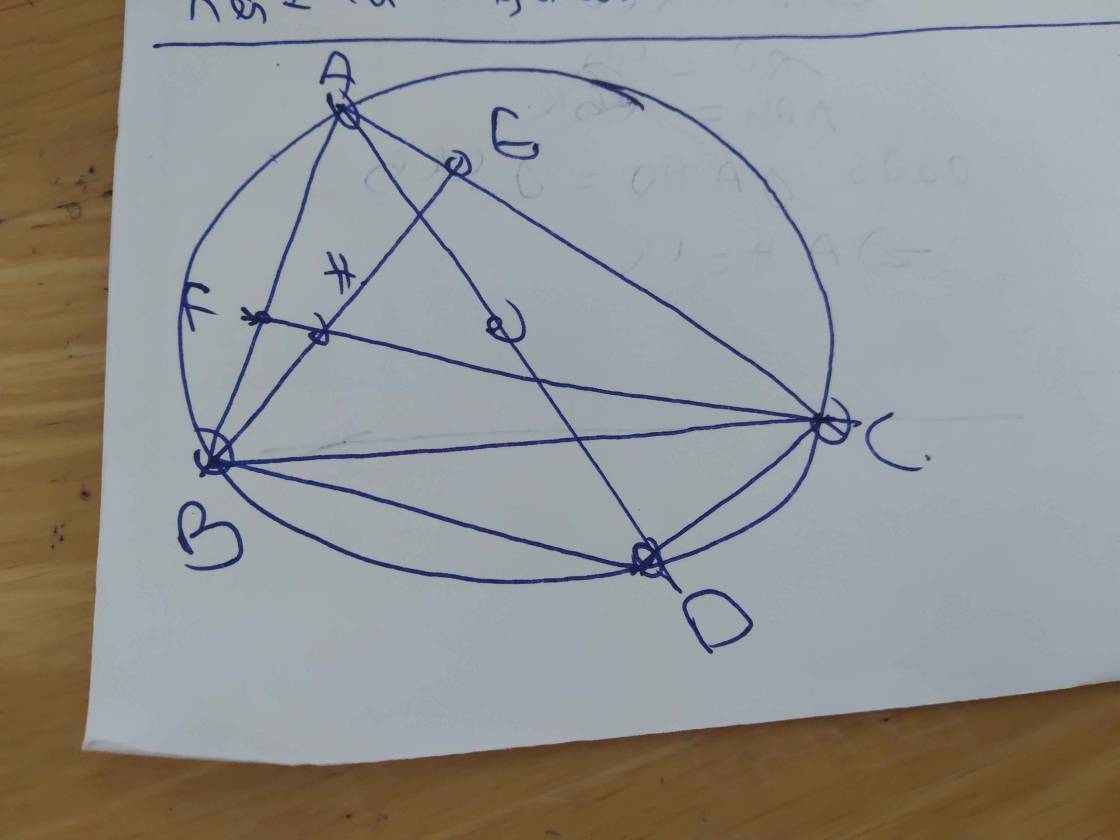
 h vẽ như sau:
h vẽ như sau: