Tìm tất cả các giá trị của m sao cho hpt sau có nghiệm
x+2y=2m+1
và 4x+2y=5m-1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 6 2015
\(\int^{x=2m+1-2y}_{4\left(2m+1-2y\right)+2y-5m+1=0}\Leftrightarrow\int^{x=2m+1-2y}_{3m+5-6y=0}\Leftrightarrow\int^{x=2m+1-\frac{3m+5}{3}}_{y=\frac{3m+5}{6}}\Leftrightarrow\int^{x=\frac{3m-2}{3}}_{y=\frac{3m+5}{6}}\)
để x,y nguyên thì 3m-2 thuộc bội của 3. 3m+5 thuộc bội của 6. mà bội là vô tận nên m cũng vô tận bạn ạ
để bài này có vẻ hơi lạ. thông thường m phải dưới mẫu cơ @@
CM
1 tháng 11 2019
x + 2 y = 2 m + 1 4 x + 2 y = 5 m − 1 ( 1 ) ( 1 ) < = > m = x + 2 y − 1 2 m = 4 x + 2 y + 1 5 = > x + 2 y − 1 2 = 3 x + 2 y + 1 5 = > 5 ( x + 2 y − 1 ) = 2 ( 4 x + 2 y + 1 ) = > 3 x − 6 y + 7 = 0
Giả sử hệ phương trình đã cho có nghiệm nguyên (x0; y0) thì
3 x 0 − 6 y 0 + 7 = 0 = > 6 y 0 − 7 = 3 x 0 ⋮ 3 = > 7 ⋮ 3 (vô lý)
Vậy hệ phương trình không có nghiệm nguyên ∀ m.
AJ
19 tháng 10 2019
mình thấy trong đề ghi vậy đó mà không biết nó có thiếu không?
CM
24 tháng 8 2018
Chọn C
Ta có bất phương trình x2- 3x+ 2≤ 0 khi và chỉ khi 1≤ x≤ 2
Yêu cầu bài toán tương đương với bất phương trình:
mx2-2( 2m+1) x+ 5m+3≤0 (1)
có nghiệm x: 1≤ x≤ 2
+ Ta đi tìm m để bất phương trình (1) vô nghiệm trên S
Tức là bpt f( x) = mx2-2( 2m+1) x+ 5m+3< 0 (2)
đúng với mọi x ∈ S
+ Nếu m= 0 (2) trờ thành: -2x+ 3≤0 hay x> 3/2 nên (2) không đúng với mọi x ∈ S
+ Nếu m≠ 0 tam thức f(x) có hệ số a= m, biệt thức ∆’ = -m2+m+ 1
Bảng xét dấu:
25 tháng 1 2021
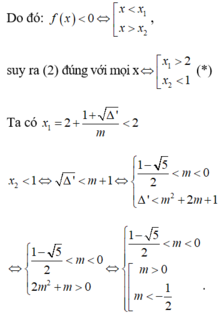
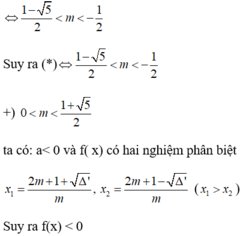
- Từ PT ( II ) ta có : \(xy\left(x+y\right)=2xy=4m^2-2m\)
\(\Rightarrow xy=2m^2-m\)
- Hệ PT trên có nghiệm là nghiệm của PT :
\(x^2-2x+2m^2-m=0\) ( I )
Có : \(\Delta^,=b^{,2}-ac=1-\left(2m^2-m\right)=-2m^2+m-1\)
- Để PT ( i ) có nghiệm \(\Leftrightarrow\Delta^,>0\)
\(\Leftrightarrow-2m^2+m-1>0\)
Vậy không tồn tại m để hệ phương trình có nghiệm .
AH
Akai Haruma
Giáo viên
26 tháng 1 2021
Phương trình (i) có nghiệm $\Leftrightarrow \Delta\geq 0$ chứ không phải $>0$ bạn nhé.