Cho (O), đường kính BC. Trên đường tròn lấy điểm A khác B và C. Gọi I là trung điểm của AB, CI cắt (O) tại E. Lấy điểm G trên đường thẳng BC sao cho \(\widehat{COI}=\widehat{CEG}\), K là trung điểm của GC, GE cắt IK tại H, BE cắt CA tại J, AE cắt BC tại F, FJ cắt CH tại D. Chứng minh DA. IC = AI. DC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1: ΔOED cân tại O
mà OH là trung tuyến
nên OH vuông góc DE
góc OHA=góc OBA=90 độ
=>O,H,B,A cùng thuộc 1 đường tròn
2: Xét ΔABD và ΔAEB có
góc ABD=góc AEB
góc BAD chung
=>ΔABD đồng dạng với ΔAEB
=>AB/AE=BD/EB
=>AB*EB=AE*BD

a) Ta có: ΔABD vuông tại A(gt)
nên A nằm trên đường tròn đường kính BD(Định lí quỹ tích cung chứa góc)
mà BD là đường kính của (O)
nên A\(\in\)(O)(Đpcm)
b) Xét (O) có
\(\widehat{AKB}\) là góc nội tiếp chắn cung AB
\(\widehat{ADB}\) là góc nội tiếp chắn cung AB
Do đó: \(\widehat{AKB}=\widehat{ADB}\)(Hệ quả góc nội tiếp)

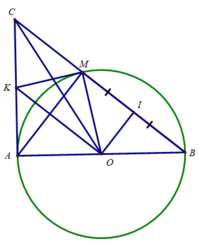
b) Tam giác ACO vuông tại A ⇒ Tâm đường tròn ngoại tiếp tam giác ACO là trung điểm của CO (1)
Xét tam giác AMB có:
I là trung điểm của AM
O là trung điểm của AB
⇒ IO là đường trung bình của tam giác AMB
⇒ IO // AM
Mà AM ⊥ MB ⇒ IO ⊥ MB
Tam giác CIO vuông tại I ⇒ Tâm đường tròn ngoại tiếp tam giác CIO là trung điểm của CO (2)
Từ (1) và (2) ⇒ 4 điểm A, I, C, O cùng thuộc một đường tròn

a: góc AEB=1/2*180=90 độ
góc FIB+góc FEB=180 độ
=>FIBE nội tiếp
b: góc ACB=1/2*180=90 độ
=>AC vuông góc DB
Xét ΔCAF và ΔCEA có
góc CAF=góc CEA
góc ACF chung
=>ΔCAF đồng dạng với ΔCEA
=>CA^2=AF*AE
Xét ΔDAB vuông tại D có AC vuông góc DB
nên CA^2=CD*CB=AF*AE

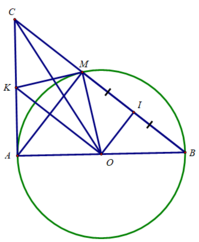
c) Tam giác CMA vuông tại M có MK là trung tuyến
⇒ MK = KA = KC
Xét Δ KAO và Δ KMO có:
KA = KM
KO là cạnh chung
AO = MO ( = bán kính (O))
⇒ Δ KAO = Δ KMO (c.c.c)
⇒ ∠(KAO) = ∠(KMO)
Mà ∠(KAO) = 90 0 ⇒ ∠(KMO) = 90 0
⇒ KM là tiếp tuyến của (O)

DC = DA
OA = OC
Do đó OD là trung trực của đoạn thẳng AC : suy ra OD vuông góc với AC
Tứ giác OECH có góc CEO + góc CHO = 180 độ
Suy ra tứ giác OECH là tứ giác nội tiếp


a) Tứ giác ACEI có: $\angle ACE+\angle EIA=90+90=180^o$ nên là tứ giác nội tiếp.
(Câu này dễ, bạn tự giải thích.)
b) Do AFEM nội tiếp nên $\angle EMB=\angle EFA=90-\angle FAB=90-\angle CAB=\angle EBM.$
Từ đó tam giác EBM cân tại E.
c) Tâm đường tròn ngoại tiếp (AEF) không chạy trên đường tròn cố định bạn nhé. Nó chạy trên đường trung trực đường thẳng AM. Ta chứng minh nó cố định. Mà A cố định nên chỉ cần chứng minh M cố định.
Từ câu b thu được I là trung điểm MB. Vậy M cách I một khoảng IB không đổi. Tức là M cố định.
Từ đó thu được đpcm.
Ps: Câu c không chắc.

