 giúp mình bài 3 và 2
giúp mình bài 3 và 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 2
a, 23 + 45 = 68
b, (-42) + (-54) = -96
c, 2025 + (-2025) = 0
d, 15 + (-14) = 1
e, 35 + (-135) = -100
Bài 3:
Tàu ngầm ở độ sâu là:
(-20) - 15 = -35 (m)
2.
a)68 b)-96 c)0
d)1 e)-100
3.
Tàu ngầm ở độ sâu là:
20+15=35(mét)
Đs:35 mét


Bài 2:
\(\left|\left|x^3-4\right|+21\right|:5=5\)
\(\Leftrightarrow\left|\left|x^3-4\right|+21\right|=25\)
\(\Leftrightarrow\left|x^3-4\right|+21=25\) hay \(\left|x^3-4\right|+21=-25\)
\(\Leftrightarrow\left|x^3-4\right|=4\) hay \(\left|x^3-4\right|=-46\) (vô lí do \(\left|x^3-4\right|\ge0\forall x\))
\(\Leftrightarrow x^3-4=4\) hay \(x^3-4=-4\)
\(\Leftrightarrow x^3-8=0\) hay \(x^3=0\)
\(\Leftrightarrow\left(x-2\right)\left(x^2+x+1\right)=0\) hay \(x=0\)
\(\Leftrightarrow\left(x-2\right)\left(x^2+2.\dfrac{1}{2}x+\dfrac{1}{4}+\dfrac{3}{4}\right)=0\) hay \(x=0\)
\(\Leftrightarrow\left(x-2\right)\left[\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}\right]=0\) hay \(x=0\)
\(\Leftrightarrow x=2\) hay \(x=0\) hay \(\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}=0\) (vô nghiệm do \(\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}>0\))
-Vậy \(S=\left\{0;2\right\}\)
Bài 3:
\(\left|\left|2x^2-2\right|+6\left|x^2-1\right|\right|=4^6:\left(2^3\right)^2\)
\(\Leftrightarrow\left|\left|2x^2-2\right|+6\left|x^2-1\right|\right|=64\)
\(\Leftrightarrow\left|2x^2-2\right|+6\left|x^2-1\right|=64\) (*) hay \(\Leftrightarrow\left|2x^2-2\right|+6\left|x^2-1\right|=-64\) (pt vô nghiệm do \(\left|2x^2-2\right|+6\left|x^2-1\right|\) luôn là số thực dương)
-Có: \(\left|2x^2-2\right|=2x^2-2\) nếu \(x\ge1\) hay \(x\le-1\).
\(\left|2x^2-2\right|=-2x^2+2\) nếu \(x\le1\) hay \(x\ge-1\).
\(6\left|x^2-1\right|=6\left(x^2-1\right)\) nếu \(x\ge1\) hay \(x\le-1\)
\(6\left|x^2-1\right|=-6\left(x^2-1\right)\) nếu \(x\le1\) hay \(x\ge-1\)
-TH1: \(x\le-1\):
(*) \(\Leftrightarrow2x^2-2+6\left(x^2-1\right)=64\)
\(\Leftrightarrow2x^2-2+6x^2-6=64\)
\(\Leftrightarrow8x^2-72=0\)
\(\Leftrightarrow x^2-9=0\)
\(\Leftrightarrow\left(x-3\right)\left(x+3\right)=0\)
\(\Leftrightarrow x=3\) (loại) hay \(x=-3\) (nhận)
-TH2: \(-1\le x\le1\):
(*) \(\Leftrightarrow-2x^2 +2-6\left(x^2-1\right)=64\)
\(\Leftrightarrow-2x^2+2-6x^2 +6=64\)
\(\Leftrightarrow-8x^2-56=0\)
\(\Leftrightarrow8x^2+56=0\) (pt vô nghiệm do \(8x^2+56\ge56\forall x\))
-TH3: \(x\ge1\):
-TH1: \(x\le-1\):
(*) \(\Leftrightarrow2x^2-2+6\left(x^2-1\right)=64\)
\(\Leftrightarrow2x^2-2+6x^2-6=64\)
\(\Leftrightarrow8x^2-72=0\)
\(\Leftrightarrow x^2-9=0\)
\(\Leftrightarrow\left(x-3\right)\left(x+3\right)=0\)
\(\Leftrightarrow x=3\) (nhận) hay \(x=-3\) (loại)
-Vậy \(S=\left\{3;-3\right\}\)

Bài 2:
3) ĐKXĐ: \(x\ge1\)Ta có: \(\sqrt{49x-49}-\sqrt{25x-25}=3\)
\(\Leftrightarrow7\sqrt{x-1}-5\sqrt{x-1}=3\)
\(\Leftrightarrow2\sqrt{x-1}=3\)
\(\Leftrightarrow\sqrt{x-1}=\dfrac{3}{2}\)
\(\Leftrightarrow x-1=\dfrac{9}{4}\)
hay \(x=\dfrac{13}{4}\)(thỏa ĐK)
Vậy: \(S=\left\{\dfrac{13}{4}\right\}\)
4) Ta có: \(1+\dfrac{3\left(x-5\right)}{4}>\dfrac{2x-1}{6}-2\)
\(\Leftrightarrow\dfrac{12}{12}+\dfrac{9\left(x-5\right)}{12}-\dfrac{2\left(2x-1\right)}{12}-\dfrac{24}{12}>0\)
\(\Leftrightarrow12+9x-45-4x+2-24>0\)
\(\Leftrightarrow5x-55>0\)
\(\Leftrightarrow5x>55\)
hay x>11
Vậy: S={x|x>11}
5) Ta có: \(\dfrac{2x+3}{x^2+1}< 0\)
mà \(x^2+1>0\forall x\)
nên 2x+3<0
\(\Leftrightarrow2x< -3\)
hay \(x< -\dfrac{3}{2}\)
Vậy: S={x|\(x< -\dfrac{3}{2}\)}


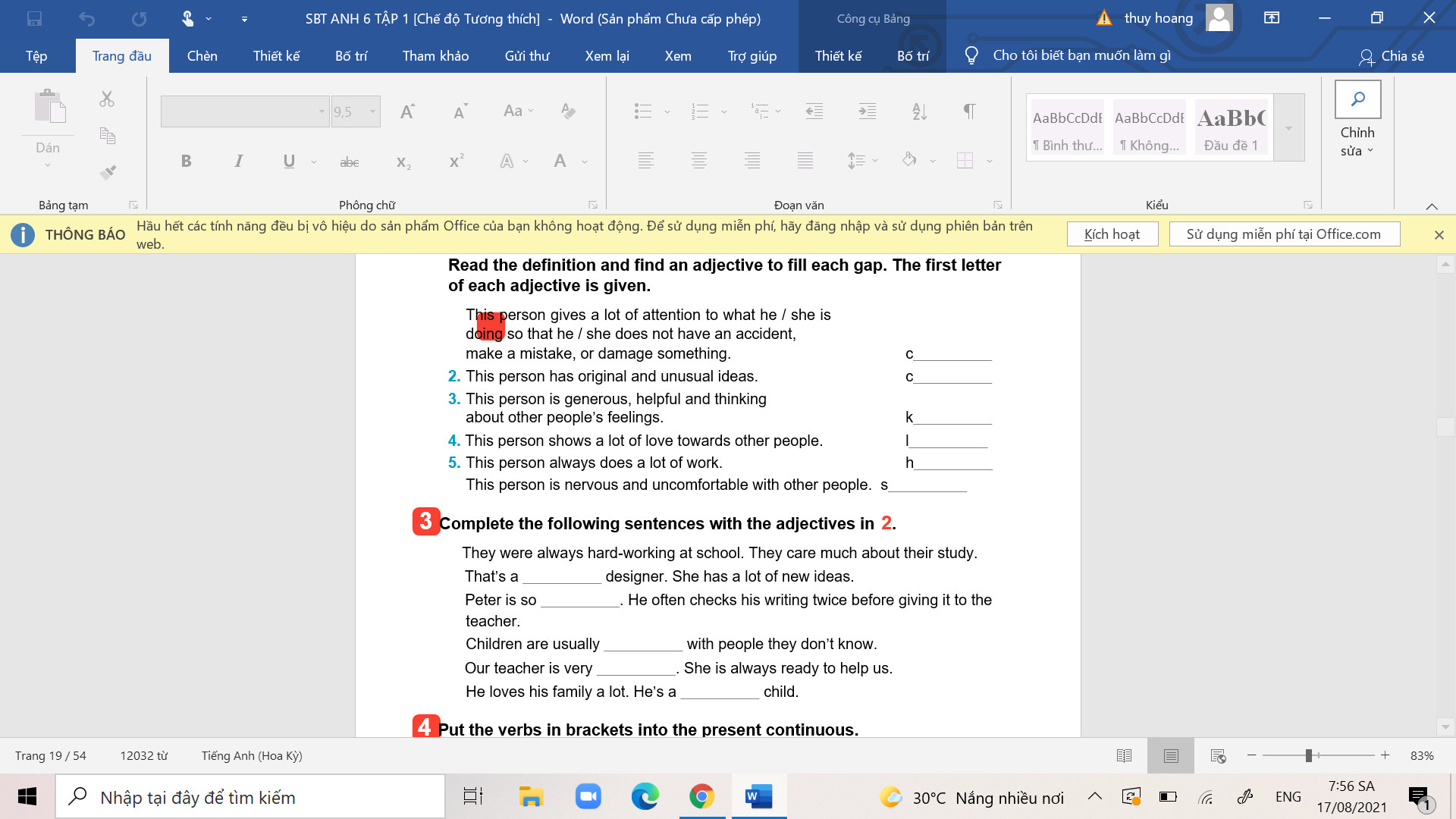 các bn giúp mình bài 2, bài 3.
các bn giúp mình bài 2, bài 3.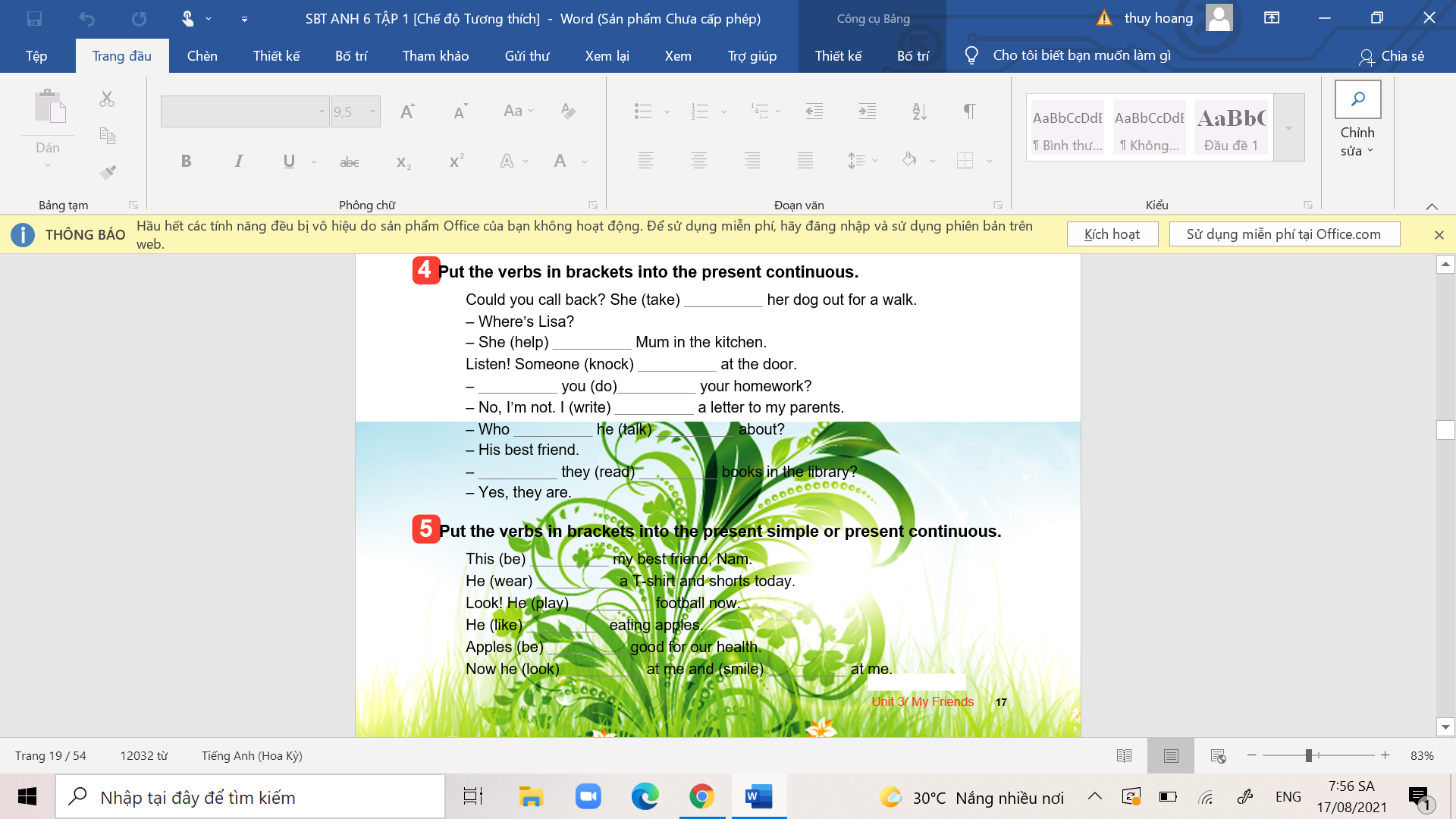 các bn giúp mình bài 4 và bài 5 nhé.
các bn giúp mình bài 4 và bài 5 nhé. 






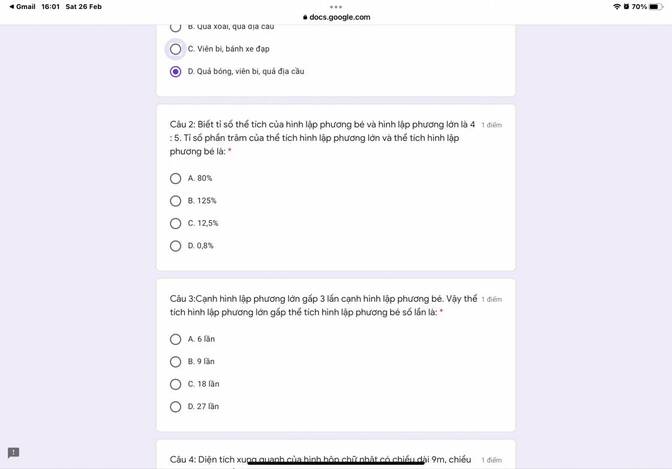


Bài 3:
5*a^2*b^3=5*(-3)^2*(-5)^3
=5*(-125)*9
=45*(-125)
=-5625