Giải phương trình nghiệm nguyên 6x²+2y2-7xy +14x-9y-21=0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
PT $\Leftrightarrow 3x^2+x(5y-8)-(2y^2+9y+4)=0$
Coi đây là pt bậc 2 ẩn $x$. Để pt có nghiệm nguyên thì:
$\Delta=(5y-8)^2+12(2y^2+9y+4)=t^2$ với $t\in\mathbb{N}$)
$\Leftrightarrow 49y^2+28y+112=t^2$
$\Leftrightarrow (7y+2)^2+108=t^2$
$\Leftrightarrow 108=(t-7y-2)(t+7y+2)$
Đến đây là dạng phương trình tích đơn giản rồi. Bạn chỉ cần xét TH. Lưu ý rằng $t+7y+2>0$ và $t-7y-2, t+7y+2$ có cùng tính chẵn lẻ.

Chọn đáp án C.
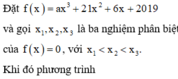
4 a x 3 + 21 x 2 + 6 x + 2019 3 a x + 21 = 9 a x 2 + 14 x + 2 2
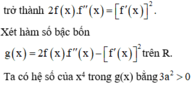
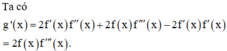
Vì f(x) = 0 có ba nghiệm phân biệt nên a ≠ 0
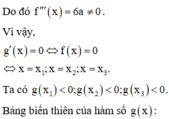
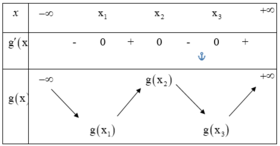
Từ bảng biến thiên, ta thấy phương trình g(x) = 0 có đúng hại nghiệm phân biệt.
Do đó phương trình 4 a x 3 + 21 x 2 + 6 x + 2019 3 a x + 21 = 9 a x 2 + 14 x + 2 2 có đúng hai nghiệm phân biệt.

Ta có \(2y^2⋮2\Rightarrow x^2\equiv1\left(mod2\right)\Rightarrow x^2\equiv1\left(mod4\right)\Rightarrow2y^2⋮4\Rightarrow y⋮2\Rightarrow x^2\equiv5\left(mod8\right)\) (vô lí).
Vậy pt vô nghiệm nguyên.
2: \(PT\Leftrightarrow3x^3+6x^2-12x+8=0\Leftrightarrow4x^3=\left(x-2\right)^3\Leftrightarrow\sqrt[3]{4}x=x-2\Leftrightarrow x=\dfrac{-2}{\sqrt[3]{4}-1}\).

Lời giải:
PT $\Leftrightarrow 3x^2+x(5y-8)-(2y^2+9y+4)=0$
Coi đây là pt bậc 2 ẩn $x$. Khi đó, để pt có nghiệm nguyên thì:
$\Delta=(5y-8)^2+12(2y^2+9y+4)=t^2$ với $t$ là số tự nhiên
$\Leftrightarrow 49y^2+28y+112=t^2$
$\Leftrightarrow (7y+2)^2+108=t^2$
$\Leftrightarrow 108=(t-7y-2)(t+7y+2)$
Đến đây là dạng pt tích đơn giản. Bạn chỉ cần xét các TH thôi với $t+7y+2>0$ và $t+7y+2, t-7y-2$ có cùng tính chẵn lẻ.

Lời giải:
PT $\Leftrightarrow x^2+x(3y-1)+(2y^2-2)=0$
Coi đây là pt bậc 2 ẩn $x$ thì:
$\Delta=(3y-1)^2-4(2y^2-2)=y^2-6y+9=(y-3)^2$. Do đó pt có 2 nghiệm:
$x_1=\frac{1-3y+y-3}{2}=-y-1$
$x_2=\frac{1-3y+3-y}{2}=2-2y$
Đến đây bạn thay vô pt ban đầu để giải pt bậc 2 một ẩn thui.

\(x^{2007}-9x^{2005}+5x^2-14x-3=0\)
\(\Leftrightarrow x^{2005}(x^{2}-9)+5x^{2}-15x+x-3=0\)
\(\Leftrightarrow x^{2005}(x-3)(x+3)+5x(x-3)+x-3=0\)
\(\Leftrightarrow (x^{2006}+3x^{2005}+5x+1)(x-3)=0\)
Xét đa thức : \(P(x)=x^{2006}+3x^{2005}+5x+1\)
\(P(x)<0\) với \(x \in \{-1;-2;-3 \}\)
\(P(x)>0\) với \(x \ge 0\) hoặc \(x \le -4\)
Vậy \(P(x) \ne 0\) \(\forall x\inℤ\)nên x = 3

a) Phương trình bậc hai 4 x 2 + 4 x + 1 = 0
Có a = 4; b’ = 2; c = 1; Δ ’ = ( b ’ ) 2 – a c = 2 2 – 4 . 1 = 0
Phương trình có nghiệm kép là:
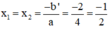
b) Phương trình 13852 x 2 – 14 x + 1 = 0
Có a = 13852; b’ = -7; c = 1;
Δ ’ = ( b ’ ) 2 – a c = ( - 7 ) 2 – 13852 . 1 = - 13803 < 0
Vậy phương trình vô nghiệm.
c) Phương trình bậc hai 5 x 2 – 6 x + 1 = 0
Có: a = 5; b’ = -3; c = 1.; Δ ’ = ( b ’ ) 2 – a c = ( - 3 ) 2 – 5 . 1 = 4 > 0
Phương trình có hai nghiệm phân biệt:
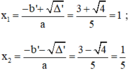
d) Phương trình bậc hai: ![]()
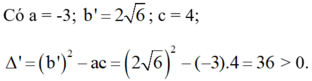
Phương trình có hai nghiệm phân biệt :
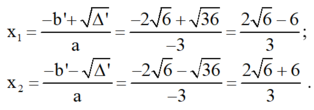
Kiến thức áp dụng
Phương trình ax2 + bx + c = 0 (a ≠ 0) có biệt thức Δ = b2 – 4ac.
+ Nếu Δ > 0, phương trình có hai nghiệm phân biệt 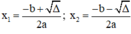
+ Nếu Δ = 0, phương trình có nghiệm kép 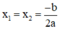 ;
;
+ Nếu Δ < 0, phương trình vô nghiệm.

\(y\in\left(-\infty;\infty\right)\)
\(-2y^2-3xy-2y+2x^2+6x=1\)
\(-2y^2-3xy-2y-2x^2+6x-1=0\)
\(-2y^2-\left(3x+2\right)y+2x^2+6x-1=0\)
\(y=\frac{\sqrt{25x^2+60x-4-3x-2}}{4}\)
\(y=-\frac{\sqrt{25x^2+60x-4+3x+2}}{4}\)
#Ứng Lân

Lời giải:
$x^2-2y^2=5\Rightarrow x$ lẻ. Đặt $x=2k+1$ với $k$ nguyên
$x^2-2y^2=5$
$\Leftrightarrow (2k+1)^2-2y^2=5$
$\Leftrightarrow 2k^2+2k-y^2=2$
$\Rightarrow y$ chẵn. Đặt $y=2t$ với $t$ nguyên
PT trở thành: $2k^2+2k-4t^2=2$
$\Leftrightarrow k^2+k-2t^2=1$
Điều này vô lý do $k^2+k-2t^2=k(k+1)-2t^2$ chẵn còn $1$ thì lẻ
Vậy pt vô nghiệm.