tìm số n để phân số A=2n+15/n+4là một số nguyên
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
MH
27 tháng 4 2022
Gọi \(d=ƯC\left(3n+15,n+4\right)\)
\(\Rightarrow\left\{{}\begin{matrix}3n+15⋮d\\n+4⋮d\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}3n+15⋮d\\3n+12⋮d\end{matrix}\right.\)
\(\Rightarrow3⋮d\)
\(\Rightarrow d\inƯ\left(3\right)=\left\{1,3\right\}\)
Thay vào
\(\Rightarrow d=1\)
27 tháng 4 2022
Để 3n+15/n+4 là PSTG thì 3n+15 chia hết cho n+4
Mà n+4 cũng chia hết cho n+4 => 3(n+4) chia hết cho n+4 =>3n+12 chia hết cho n+4
=>(3n+12)-(3n+4) chia hết cho n+4
=>3n+12-3n-4 chia hết cho n+4
=>8 chia hết cho n+4
=>n+4 thuộc Ư(8)={1; -1 ;2; -2 ;4; -4 ;8; -8 } , ta có bản
| n+4 | 1 | -1 | 2 | -2 | 4 | -4 | 8 | -8 |
| n | -3 | -5 | -2 | -6 | 0 | -8 | 4 | -12 |
Vậy n = {-3; -5; -2; -6; 0; -8; 4; -12}
VT
1
6 tháng 5 2015
\(\frac{2n+15}{2n-1}=\frac{2n-1+16}{2n-1}=1+\frac{16}{2n-1}\)
Để phân số trên nguyên \(\Leftrightarrow\frac{16}{2n-1}\) nguyên.
\(\Leftrightarrow2n-1=Ư\left(16\right)=\left\{-16;-8;-4;-2;-1;1;2;4;8;16\right\}\)
Rồi bạn tự tìm n nha !
DB
1
NN
22 tháng 1 2024
a, Để \(\dfrac{n+1}{n-2}\) có giá trị là một số nguyên thì n + 1 ⋮ n - 2
=> (n - 2) + 3 ⋮ n - 2
Vì (n - 2) ⋮ n - 2 nên 3 ⋮ n - 2
=> n - 2 ∈ Ư(3) ∈ {-3;-1;1;3}
=> n ∈ {-1;1;3;5}
b, Để \(\dfrac{4n+5}{2n-1}\) có giá trị là một số nguyên thì 4n + 5 ⋮ 2n - 1
=> (4n - 2) + 7 ⋮ 2n - 1
=> 2(2n - 1) + 7 ⋮ 2n - 1
Vì 2(2n - 1) ⋮ 2n -1 nên 7 ⋮ 2n - 1
=> 2n - 1 ∈ Ư(7) ∈ {-7;-1;1;7}
=> n ∈ {-3;0;1;4}
VT
1
VA
9 tháng 5 2016
Ta có 2n+15 = 2n+2+13 = 2.(n+1) + 13
Để p/số có giá trị là số nguyên thì 2n+15 chia hết cho n+1 hay 2.(n+1) +13 chia hết cho n+1 mã 2.(n+1) chia hết cho n+1 nên 13 chia hết cho n+1 suy ra n+1 thuộc Ư(13)
Mả U(13) = {-13;-1;1;13} suy ra n+1 thuoc{-13;-1;1;13}
Vì n thuộc Z nên ta có bảng sau
| n+1 | -13 | -1 | 1 | 13 |
| n | -14 | -2 | 0 | 12 |
| n/xét | chon | chon | chon | chon |
Vậy với n thuộc { -14;-2;0;12} thì p/số có giá trị là số nguyên
k nha !!!!!
ND
2
TM
9 tháng 5 2016
phân số 2n+15/n+1 là một số nguyên
=> 2n+15 chia hết cho n+1
=> 2n+2+13 chia hết cho n+1
=> 2(n+1)+13 chia hết cho n+1
=> 13 chia hết cho n+1
=> n+1 \(\in\){-13;-1;1;13}
=> n\(\in\){-14;-1;0;12}
HN
1
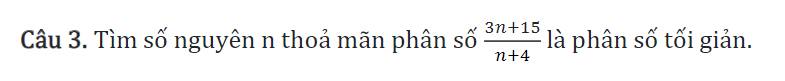
\(A=\dfrac{2n+15}{n+4}\left(n\in Z,n\ne-4\right)\\ A=\dfrac{2\left(n+4\right)+7}{n+4}=2+\dfrac{7}{n+4}\\ A\in Z=>\dfrac{7}{n+4}\in Z\\ =>n+4\inƯ\left(7\right)=\left\{\pm1;\pm7\right\}\\ =>n\in\left\{-3;-5;3;-11\right\}\left(TM\right)\)
giup minh voi