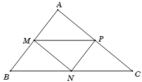
Cho tam giác ABC có M,N,P lần lượt là các trung điểm của các cạnh BC,AC,AB.
Chứng minh :
a) NP//BC và NP = BC/2
b) Bốn tam giác APN,PBM,NMC,MPN bằng nhau
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TG
3 tháng 3 2021
Tam giác ABC có:
+) N là trung điểm của AC
+) M là trung điểm của BC
=> MN là ĐTB của tam giác ABC
Tương tự c/m:
+) PN là ĐTB của tam giác ABC+) PM là ĐTB của tam giác ABC
*Có: MN là ĐTB của tam giác ABC
\(\Rightarrow MN=\dfrac{1}{2}AB\)
\(\Rightarrow\dfrac{MN}{AB}=\dfrac{\dfrac{1}{2}AB}{AB}=\dfrac{1}{2}\)
Có: PN là ĐTB của tam giác ABC
\(\Rightarrow PN=\dfrac{1}{2}BC\)
\(\Rightarrow\dfrac{PN}{BC}=\dfrac{\dfrac{1}{2}BC}{BC}=\dfrac{1}{2}\)
Có: PM là ĐTB của tam giác ABC
\(\Rightarrow PM=\dfrac{1}{2}AC\Rightarrow\dfrac{PM}{AC}=\dfrac{\dfrac{1}{2}AC}{AC}=\dfrac{1}{2}\)
Xét tam giác MNP và tam giác ABC có:
\(\dfrac{MN}{AB}=\dfrac{NP}{BC}=\dfrac{MP}{AC}\left(=\dfrac{1}{2}\right)\)
7 tháng 11 2021
Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Suy ra: BC=2MN
hay BC=6(cm)
29 tháng 11 2021
a: Xét tứ giác ADCP có
N là trung điểm của AC
N là trung điểm của DP
Do đó: ADCP là hình bình hành
7 tháng 11 2021
a: Xét tứ giác ADCP có
N là trung điểm của AC
N là trung điểm của DP
Do đó: ADCP là hình bình hành
15 tháng 1
M là điểm chính giữa của cạnh AC
=>M là trung điểm của AC
N là điểm chính giữa của cạnh AB
=>N là trung điểm của AB
P là điểm chính giữa của cạnh BC
=>P là trung điểm của BC
Xét ΔAMN và ΔACB có
\(\dfrac{AM}{AC}=\dfrac{AN}{AB}\left(=\dfrac{1}{2}\right)\)
\(\widehat{A}\) chung
Do đó: ΔAMN đồng dạng với ΔACB
=>\(\dfrac{S_{AMN}}{S_{ACB}}=\left(\dfrac{AM}{AC}\right)^2=\dfrac{1}{4}\)
=>\(S_{AMN}=\dfrac{1}{4}\cdot120=30\left(cm^2\right)\)
Xét ΔBNP và ΔBAC có
\(\dfrac{BN}{BA}=\dfrac{BP}{BC}\left(=\dfrac{1}{2}\right)\)
\(\widehat{B}\) chung
Do đó: ΔBNP~ΔBAC
=>\(\dfrac{S_{BNP}}{S_{BAC}}=\left(\dfrac{BN}{BA}\right)^2=\dfrac{1}{4}\)
=>\(S_{BNP}=\dfrac{1}{4}\cdot120=30\left(cm^2\right)\)
Xét ΔCPM và ΔCBA có
\(\dfrac{CP}{CB}=\dfrac{CM}{CA}\left(=\dfrac{1}{2}\right)\)
\(\widehat{C}\) chung
Do đó: ΔCPM~ΔCBA
=>\(\dfrac{S_{CPM}}{S_{CBA}}=\left(\dfrac{CP}{CB}\right)^2=\dfrac{1}{4}\)
=>\(S_{CPM}=\dfrac{1}{4}\cdot120=30\left(cm^2\right)\)
Ta có: \(S_{ANM}+S_{BNP}+S_{NMP}+S_{MPC}=S_{ABC}\)
=>\(S_{MPN}+30+30+30=120\)
=>\(S_{MPN}=30\left(cm^2\right)\)
nên 
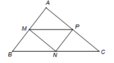
a: Xét ΔABC có P,N lần lượt là trung điểm của AB,AC
nên PN là đường trung bình
=>PN//BC và PN=BC/2=BM
b: Xét ΔAPN và ΔPBM có
AP=PB
góc APN=góc PBM
PN=BM
=>ΔAPN=ΔPBM
Xét ΔPBM và ΔNMC có
PB=NM
góc PBM=góc NMC
BM=M
=>ΔPBM=ΔNMC
Xét ΔMPN và ΔPBM có
MP=PB
PM chung
PN=BM
=>ΔMPN=ΔPBM