122+(-22)+(-1)+25.4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LK
1
H9
HT.Phong (9A5)
CTVHS
30 tháng 6 2023
\(A=-5^{22}\left\{-222\left[-122-\left(100-5^{22}\right)+2022\right]\right\}\)
\(A=-5^{22}\left\{-222\left[1900-\left(100-5^{22}\right)\right]\right\}\)
\(A=-5^{22}\left[-222\left(1900-100+5^{22}\right)\right]\)
\(A=-5^{22}\left[-222\left(1800+5^{22}\right)\right]\)
\(A=-5^{22}\left(-399600-222\cdot5^{22}\right)\)
\(A=399600\cdot5^{22}+222\cdot5^{44}\)
TH
1
AH
Akai Haruma
Giáo viên
13 tháng 11 2023
Lời giải:
$=5^{22}-22+[122-(100+5^{22})+2022]$
$=5^{22}-22+122-100-5^{22}+2022$
$=(5^{22}-5^{22})+(-22+122-100)+2022$
$=0+0+2022=2022$
24 tháng 12 2016
Tổng là:
122 + 22 = 144
Đáp số:144
Chúc giáng sinh vui vẻ
DT
8 tháng 11 2023
`(3x+1)^2=25.4`
<=> `(3x+1)^2=10^2`
<=> `3x+1=10` hoặc `3x+1=-10`
<=> `x=3` hoặc `x=-11/3`
PT
5
HA
15 tháng 1 2017
1+1+1+1+11+11+25.4+10+5+1
=4+11.2+25.4+10+6
=4+6+10+100+121
=10+10+221
=20+221
=241
k mình nha!
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 7 2020
\(22^n=2^n.11^n\)
\(122!=1.2...11...22...33...44...55...66...77...88...99...110...121\)
\(=11^{11}.A\)
\(\Rightarrow n_{max}=11\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
18 tháng 11 2023
A = - 522 - { - 222 - [ - 122 - (100 - 522) + 2022] }
A = - 522 - { -222 - [- 122 - 100 + 522 ] + 2022}
A = - 522 - { -222 - { - 222 + 522 } + 2022}
A = - 522 - {- 222 + 222 - 522 + 2022}
A = -522 + 522 - 2022
A = - 2022
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
18 tháng 11 2023
B = 1 + \(\dfrac{1}{2}\)(1 + 2) + \(\dfrac{1}{3}\).(1 + 2 + 3) + ... + \(\dfrac{1}{20}\).(1 + 2+ 3 + ... + 20)
B = 1+\(\dfrac{1}{2}\)\(\times\)(1+2)\(\times\)[(2-1):1+1]:2+ ... + \(\dfrac{1}{20}\)\(\times\) (20 + 1)\(\times\)[(20-1):1+1]:2
B = 1 + \(\dfrac{1}{2}\) \(\times\) 3 \(\times\) 2:2 + \(\dfrac{1}{3}\) \(\times\)4 \(\times\) 3 : 2+....+ \(\dfrac{1}{20}\) \(\times\)21 \(\times\) 20 : 2
B = 1 + \(\dfrac{3}{2}\) + \(\dfrac{4}{2}\) + ....+ \(\dfrac{21}{2}\)
B = \(\dfrac{2+3+4+...+21}{2}\)
B = \(\dfrac{\left(21+2\right)\left[\left(21-2\right):1+1\right]:2}{2}\)
B = \(\dfrac{23\times20:2}{2}\)
B = \(\dfrac{23\times10}{2}\)
B = 23
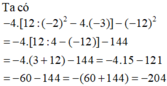
\(122+\left(-22\right)+\left(-1\right)+25.4\)
\(=122-22-1+100\)
\(=199\)
`122+(-22)+(-1)+25xx4`
`=122-22-1+100`
`=100-1+100`
`=100+100-1`
`=200-1`
`=199`